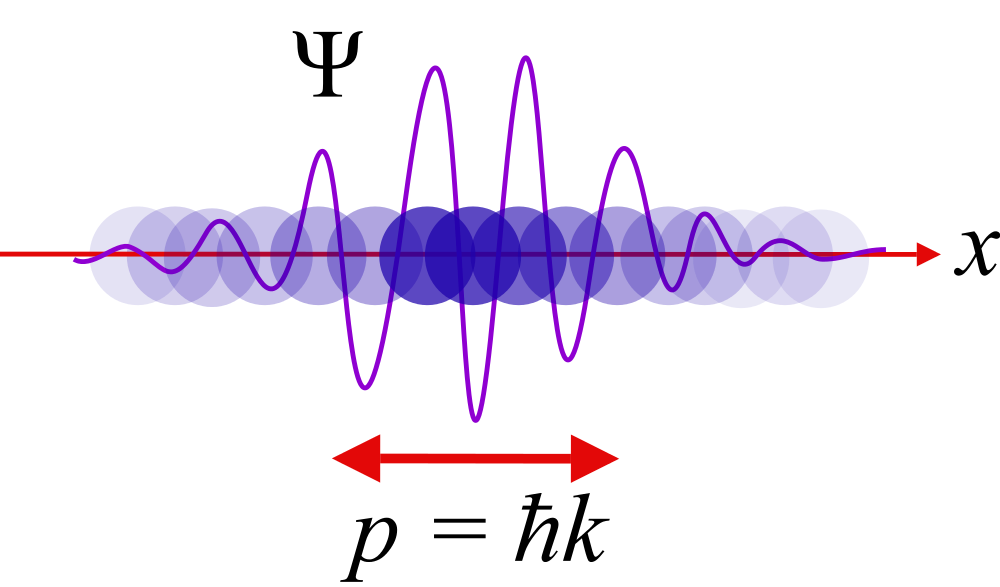
Caption: A cartoon illustrating the wave-particle duality of quantum mechanics.

Features:

1. You see a wave packet (a wave pulse of varying wavelength) with a superimposed set of balls of varying brightness.

2. The balls representing the "density of being" of a single particle: the brighter the ball, the higher the "density of being".
   The balls do NOT represent motion in a quasi stroboscopic way in this case.

3. In quantum mechanics, a particle exists in a superposition of positions---so much here, so much there.

   How much here or there is its "density of being"---which is just a useful nonce expression.

   Conventionally, the "how much here or there" is called a probability distribution, but that may NOT be exactly right as we discuss below.

4. The wave function of quantum mechanics determines/describes the "density of being".

   The capital Greek Psi = Ψ (pronounced Psi like sigh) is the common symbol for the wave function.

   The "density of being" itself is the QM probabilitiy density which is equal to the square of the complex-number absolute value of the wave function: i.e., = |Ψ|**2.

   The QM probabilitiy density is, among other things, the probability density for measuring a particle at any point in space.

5. In the cartoon, the particle's "density of being" goes to zero asymptotically at the edges of the cartoon. It is also exactly zero at the nodes or (AKA zeros) of the wave function.

6. The p=ħk in the cartoon stands for the mean momentum of the particle.

   The ħ (pronounced h-bar) is the reduced Planck's constant ħ = (1.054571817 ...)*10**(-34) J-s = (6.582119569 ...)*10**(-16) eV (exact values) (see NIST: Fundamental Physical Constants --- Complete Listing) (which is a universal physical constant that first turned up in quantum mechanics) and k is the mean wavenumber.

   k=2π/λ where λ is the mean wavelength.

   A wavelength is the length of one complete up-and-down cycle.

7. Whether the wave function is a real physical object OR is just informational (like a probability distribution, e.g., for dice: see file dice_probability.html) OR is somewhere in between has been debated since the dawn of quantum mechanics in 1925--1926.
   "Somewhere in between" may be that the wave function is an approximation to a real thing that works extremely well as an information giver.

8. Personally, yours truly thinks of it as a real physical object---but what does yours truly know---but yours truly is NOT alone.

   The megaminds have been divided on many interpretational issues in quantum mechanics---and have been since Albert Einstein (1879--1955) and Niels Bohr (1885--1962) had their iron-cage grudge matches on the interpretational issues.

   But it doesn't seem to matter how we interpret quantum mechanics---it works just fine no matter what we think of it.

9. It's amazing that what is arguably the best verified of all physical theories is perpetually interpretationally elusive.
   We are down to polls on the issues---which is a heck of a way to do science.

   See Schlosshauer et al., 2013, A Snapshot of Foundational Attitudes Toward Quantum Mechanics.

   Yours truly jests---polls are pretty common in science before the evidence solidifies---but with quantum mechanics, the evidence never solidifies.

10. And quantum mechanics is the best verified physical theory---it is never wrong---there are approximations, often severe---there are mistakes in calculations and experiments---but NO anomaly has ever resisted attack---it is never wrong---your cell phone would NOT work if quantum mechanics did NOT work the way we think it does.