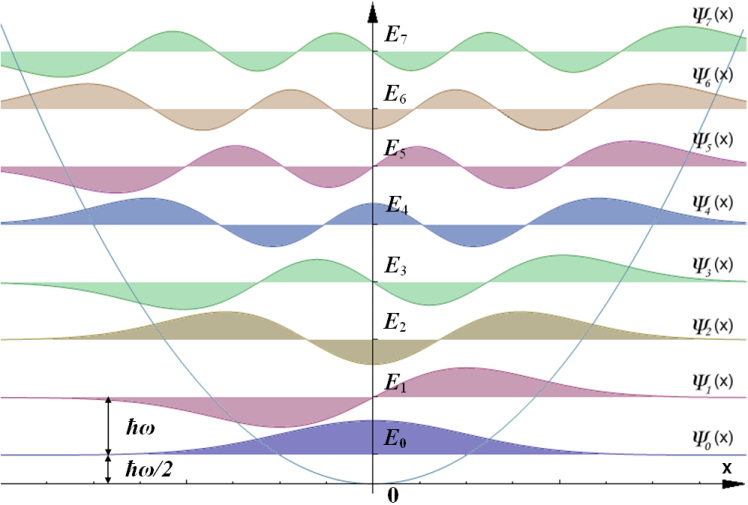
Caption: A diagram illustrating key features of the 1-dimensional quantum harmonic oscillator.

Features:

1. The horizontal axis represents the single direction of motion for a 1-dimensional physical system.

2. The blue curve is the potential (i.e., potential energy or energy of position) of a particle.

3. The harmonic oscillator potential is a quadratic: i.e., V=(1/2)kx**2, where k is a constant.

   Note the ideal harmonic oscillator potential extends to ±∞, and so all particles are bound.

   Realistic harmonic oscillator potentials only extend a finite distance, and so particles can escape if they have enough energy.

4. The vertical direction represents the energy of the quantized energy levels.

   The allowed energy levels obey the formula

         E = (n+1/2)ħω ,

   where n is an integer quantum number (dimensionless number or unitless number) that runs 0, 1, 2, 3, ... , ħ (vocalized h-bar) is the Planck constant divided by 2π, and ω is the reference angular frequency of the system.

   Only the first 8 energy levels are displayed.

   The ideal quantum harmonic oscillators has an infinite number of energy levels.

   Realistic quantum harmonic oscillators transition to non-harmonic oscillator potentials as one moves away from the equilibrium point (here x=0 point) and eventually the potentials stop growing. Thus, eventually ones reaches unbounded states as energy increases to the point where the particle can escape the potential well and go off to infinity.

5. The fact that the energy levels are equally spaced in energy is a remarkable feature of the quantum harmonic oscillator.

   No other simple potential gives equal spacing.

   The supersymmetric (SUSY) harmonic oscillator potentials also give equally spaced energy levels, but they arn't so simple.

6. Superimposed on the energy level lines are the corresponding wave functions (Ψ_0, Ψ_1, ... ) for the quantum harmonic oscillator.

   The wave functions do NOT extend in the energy dimension. They have there own axis unit. Their superposition here is to concretely illustrate their behavior and their energy simultaneously.

   The diagram doesn't clarify if the wave functions are relatively to-scale or not.

   The wave functions are positive above their respective energy level line and negative below.

7. The probability density (which might be more accurately called the existence density) for the particle is the complex-number absolute value of the wave function: |Ψ_n|**2.

8. As one can see the wave functions are oscillatory with nodes (where the probability density is zero) and anti-nodes (where the probability density has a local local maximum.

9. The harmonic oscillator potential is not a sharp boundary to the region of allowed oscillations like the endpoints of vibrating string. It gives a spread-out or soft boundary.

   Nevertheless, the boundary provided by harmonic oscillator potential enforces quantization.

   Thus, only an integer number of wavelengths of the wave function can be fit with the harmonic oscillator potential's potential well.

   The wavelengths of the standing waves do vary though as the diagram shows.