Image 1 Caption: An animation illustrating on the left side the apparent retrograde motion of an outer planet (e.g., Mars) in a heliocentric solar system model) and on the right side spatial retrograde motion giving rise to apparent retrograde motion in an epicycle model in a geocentric solar system model (e.g., the Ptolemaic system).

Features:

1. The Sun is yellow, the Earth is blue, and the outer planet is red.

2. The relative motion of the Sun and Earth are the same in both cases, but NOT that of the outer planet and Earth. In the geocentric case, the outer planet really does orbit Earth on a deferent with an epicycle. The individual deferent and epicycle motions are NOT shown, but they are shown in Image 2 below.

   

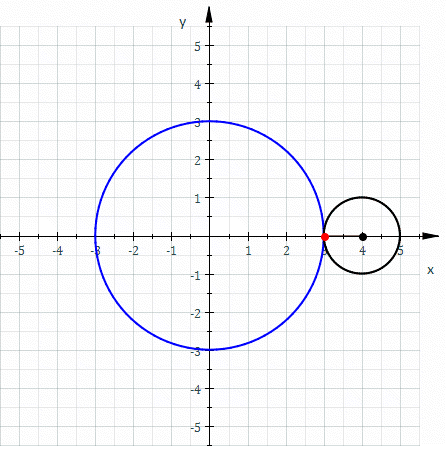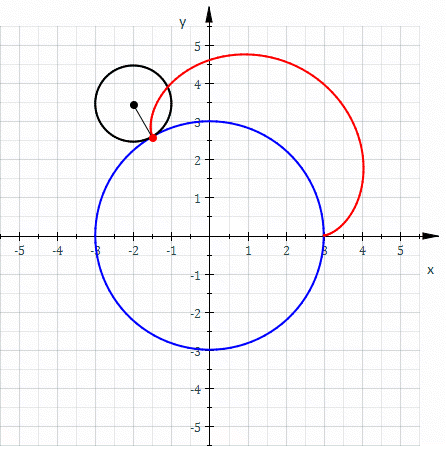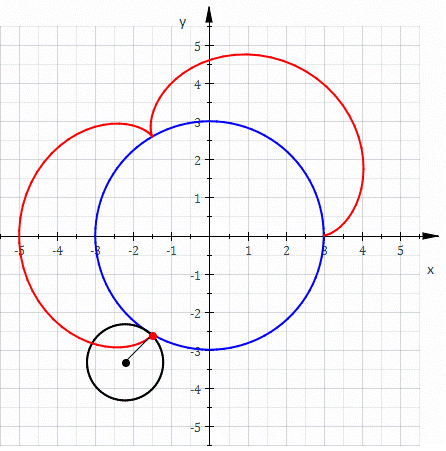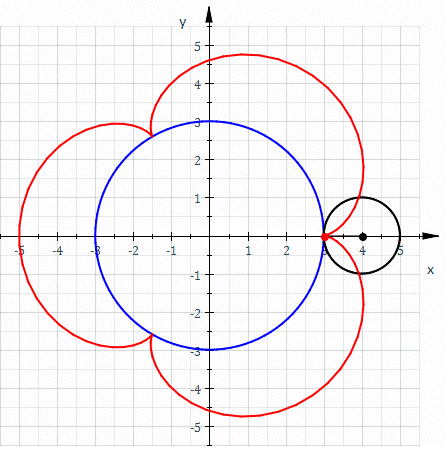
3. Image 2 Caption: An animation where "The red curve is an epicycloid traced as the small circle (radius r = 1) rolls around the outside of the large circle (radius R = 3)." This animation does NOT depict an actual planet epicycle model since there are 3 apparent retrograde motions and actual planet epicycle models had only 1 apparent retrograde motions when in inferior conjunction (for inferior planets) or in opposition (for superior planets).

4. Image 1 Caption Continued: The ratio of inner object to outer object orbital periods in both cases is 1:2. The 1:2 ratio was chosen to give the systems an simple cycling behavior.

5. In the heliocentric case, the apparent retrograde motion happens when the Earth passes the outer planet on the inside track. This necessarily means that the outer planet is in opposition during its apparent retrograde motion.

6. In the geocentric case, spatial retrograde motion gives rise to apparent retrograde motion. The spatial retrograde motion is a result of the epicycle motion superimposed on the deferent motion. The initial conditions are chosen such that the outer planet is in opposition during its spatial retrograde motion.

7. As we believe that correlated motions require physical causes, it is clear that the heliocentric case is easier to explain. Two relatively small planets are somehow forced to orbit the large Sun in circular orbits. The relatively small planets do NOT affect each other to 1st order and their motions are circular orbits around the relatively large Sun.

8. The geocentric case is harder to explain by physical causes. Somehow the small Earth makes the Sun orbit it in a circular orbit and the outer planet orbit it in a complex deferent-epicycle orbit. Also the Sun and outer planet motions are somehow correlated.

9. It is easy to see why those people in the 16th century and 17th century who were trying to understand the Solar System in terms of physical causes were led to favor the heliocentric solar system model over the geocentric solar system model.

Images:

1. Credit/Permission: © Cleon Teunissen (AKA User:Cleonis), 2011 / Creative Commons CC BY-SA 2.5.
   Image link: Wikipedia: File:Apparent retrograde motion.gif.
   
2. Credit/Permission: © User:Sam Derbyshire, 2008 (uploaded to Wikimedia Commons by User:Gengiskanhg, 2021) / CC BY-SA 3.0.
   Image link: Wikimedia Commons: File:EpitrochoidOn3-generation.gif.