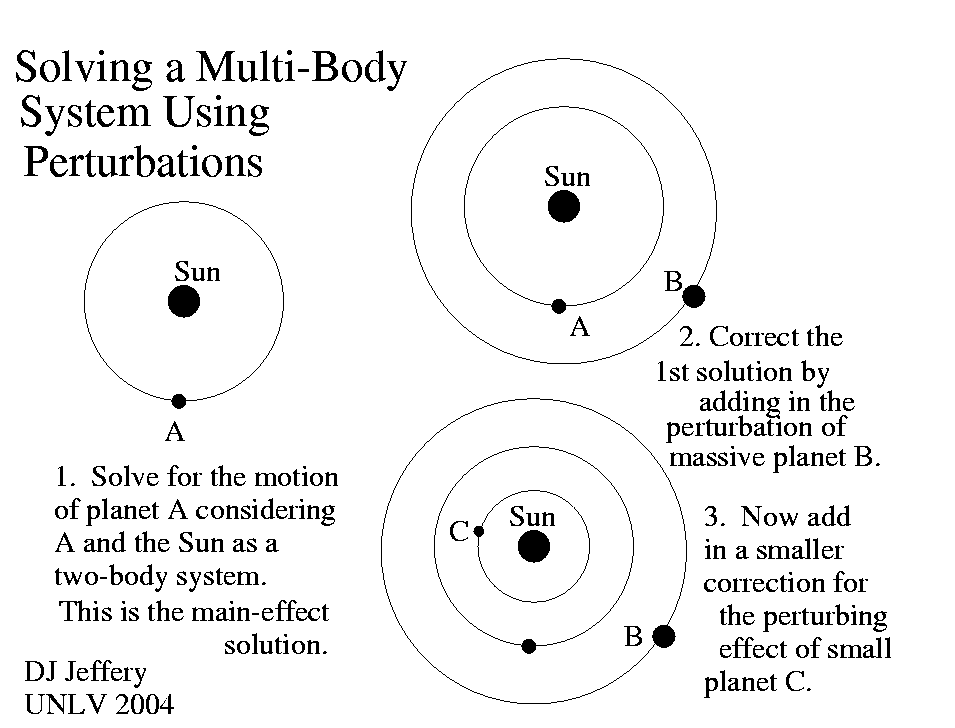
Caption: A diagram illustrating the solution of an astrophysical self-gravitating multi-body system (AKA n-body system) by perturbation theory.

The procedure of perturbation theory for multi-body systems is as follows:

1. You first solve exactly a simplified multi-body system that approximates the real multi-body system.

   This gives an approximate solution to the real multi-body system.

   Usually, the simplication is to treat each astro-body as part of a (gravitational) two-body system (for which an exact solution exists).

2. Then you correct your calculation by adding on in order of decreasing importance the previously excluded effects of the real multi-body system as astronomical perturbations to the exact solution for the simplified multi-body system.

   The astronomical perturbations make the simplified multi-body system more like the real multi-body system and improve the approximate solution.

3. There is usually NO end to the series of astronomical perturbations of decreasing importance.

   Note, perturbation theory will always be NOT exactly correct because of round-off error in floating-point arithmetic and truncation error (in a series expansion): perturbation theory is a series expansion solution. You just stop adding astronomical perturbations to the series expansion solution and when your solution is adequate: i.e., is sufficiently accurate/precise for yours needs. Often you stop adding astronomical perturbations when your approximate solution agrees with observations to within observational error.

4. For astrophysical systems, the astronomical perturbations are usually overwhelmlingly gravitational perturbations.