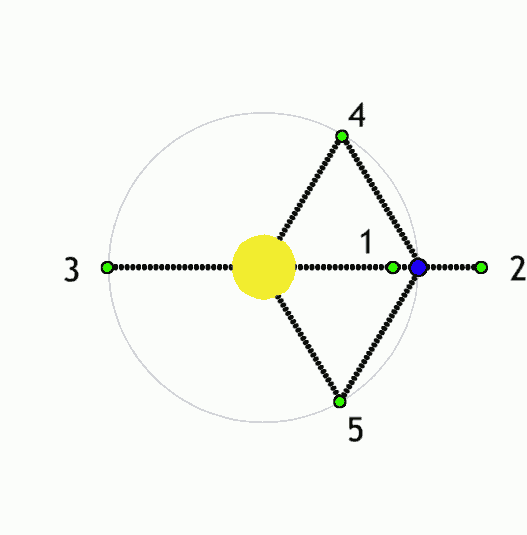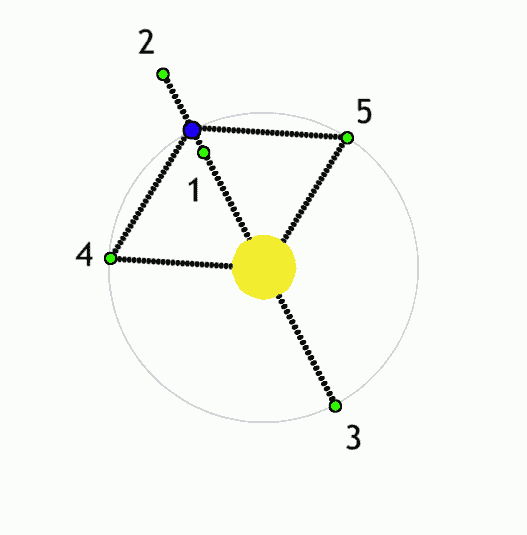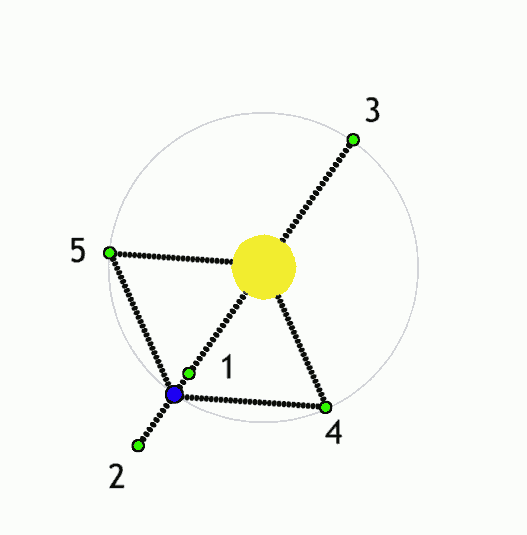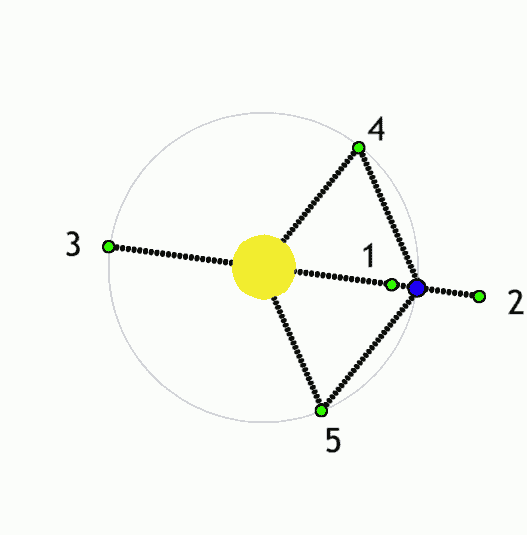
Image 1 Caption: An animation showing the motion of the 5 Lagrange points (L-points) in a corotating reference frame specified by the circular orbits of 2 large astro-bodies around their mutual center of mass (CM). The of 2 large astro-bodies determine the 5 L-points).

Features:

1. The 5 L-points of a (gravitationally bound) 2-finite-body system are points of mechanical equilibrium for test particles (i.e., astro-bodies which are negligible in mass relative to the masses of the 2 finite bodies) in the a corotating reference frame established by the 2 finite bodies.

   In the special case of the animation, the 2 bodies are in astro-bodies around their mutual center of mass (CM).

2. To be clear, the Lagrange points corotate with the 2 large astro-bodies.

3. Image 2 Caption: The 5 L-points Sun-Earth 2-body system and the trajectory of the Gaia spacecraft (mission 2013--2025?) from Earth to the L2 point where it went into Lissajous orbit (which we describe below).

4. The mechanical equilibria are due to a combination of the gravitational forces, the centrifugal force, and, for the L4 and L5 points, the Coriolis force (see Wikipedia: Lagrange point: Stability).

   Lagrange points are most easily understood for circular orbits for the 2 bodies are in astro-bodies and that is all we will consider in here.

5. The L1, L2, and L3 points are collinear with the 2 finite bodies.

   The L4 and L5 points complete equilateral triangles with the 2 finite bodies. This means they are 60° away from the line joining the 2 finite bodies as seen from either of the 2 finite bodies.

6. The 3 collinear Lagrange points were discovered by Leonhard Euler (1707--1783) and the other 2 by Joseph-Louis Lagrange (1736--1813) (see Wikipedia: Lagrange points: History). Both persons are famous mathematicians and are the eponyms of many things in mathematics and physics: e.g., Euler's formula, Euler's number (much more commonly known as the exponential number e = 2.71828 ... ), the Euler-Lagrange equation, the Euler-Mascheroni constant γ = 0.5772156649 ... , Lagrangian mechanics, and Lagrange multipliers.

7. The L1, L2, and L3 points are unstable equilibria (see Wikipedia: Lagrangian point: Stability). In principle, any perturbation, NO matter how small, will cause test particles to escape to infinity.

8. The L4 and L5 points are stable equilibria due to the Coriolis force (see Wikipedia: Lagrange point: Stability).

   A stable equilibrium is one where motions due sufficiently small perturbation on a test particle placed at the stable equilibrium damp out and the test particle average position remains the stable equilibrium. The test particle NEVER escapes to infinity.

9. In fact, all physically real stable equilibria are metastable (i.e., a large enough perturbation will cause a test particle to escape to infinity) and most (maybe all) physically real unstable equilibria are slightly metastable (i.e., a small enough perturbation will NOT cause a test particle to escape to infinity). However, we customarily do NOT use the term metastable state unless the state is obviously NOT near the limits of absolute stability or instability.

10. In planetary systems, each planet and its star establishes Lagrange points.

    However, the gravitational perturbations of an n-body system with more than 2 astro-bodies make the Lagrange points less than ideal. In general, the larger planet, the larger its gravitational force, and the more ideal its Lagrange points.

    For example, in the Solar System, Jupiter's L4 and L5 points are particularly close to ideal, and therefore very stable equilibria. For that reason, Jupiter's trojan asteroids accumulated near its L4 and L5 points and tended to stay there over the Solar System's evolution.

    The word trojan has come to mean any small astro-body (e.g., an asteroid) that orbits near L4 and L5 points.

11. Now test particles can be kept at the L1 point, L2 point, and L3 point by orbital station-keeping using orbital maneuvers (AKA burns) using thruster burns (see also Wikipedia: Thrust, Wikipedia: Rocket, Wikipedia: Rocket engine, and Wikipedia: Spacecraft propulsion).

12. In fact, the Earth's Lagrange points Lagrange points have become favorite locations for spacecraft for special space missions

13. In practice, it turns out that for some space missions, it is better to put spacecraft into Lissajous orbits (or their special case halo orbits) around L-points rather than at L-points. Lissajous orbits are quasi-periodic orbits around L-points that are NOT in the orbital plane of the 2-body system. In quasi-periodic orbits the orbiting astro-body is bound, but the orbital trajectory never exactly repeats (see also Wikipedia: Orbit dynamics: asymptotically periodic orbit).

    Lissajous orbits are sort of like quasi-periodic epicycles come to life.

    Lissajous orbits can used for spacecraft at the unstable L1 point, L2 point, and L3 point

14. The Earth's Lagrange point the L2 point is currently a particular favorite for important space missions.

    This L2 point is on Earth-Sun line at 0.010 AU (∼ 1.5*10**6 km) from the Earth.

    An astro-body at that distance from the Sun, NOT at an L2 point would have an orbital period about the Sun that is slightly longer than a sidereal year = 365.256363004 days (J2000).

    An astro-body in Lissajous orbit about L2 has, of course, an orbital period about the Sun of exactly a sidereal year = 365.256363004 days (J2000).

15. Note that Earth's umbra extends out to ∼ 0.009 AU (∼ 1.4*10**6 km) (see Wikipedia: Umbra, penumbra and antumbra: Umbra; Richard Pogge: Lecture 9: Eclipses of the Sun & Moon: scroll down ∼ 25 %).

    So spacecraft at the L2 point are NEVER in the umbra. In fact, their Lissajous orbits probably NEVER put them in the penumbra either.

    Going into penumbra would decrease the solar power that powers most spacecraft.

16. Examples of spacecraft at the Earth's Lagrange points:
    1. At the L2 point, Gaia spacecraft (mission 2013--2025?) (see also gaia_2013_2025.html), the James Webb Space Telescope (JWST; 2021--2041?), and Euclid spacecraft (2023--2029?) (see also videos Euclid in a nutshell (2023) | 1:14, The Euclid Space Telescope: tackling dark matter and dark energy mysteries (2023) | 14:54, etc.).

    2. The 2 Lagrange spacecrafts (est. 2020s--2030s), one at L1 and one at L5 (see Wikipedia: Lagrange spacecrafts: Overview): The European Space Agency (ESA) is planning two spacecraft, the Lagrange spacecrafts (est. 2020s--2030s), which will study solar weather (and space weather generally) and in particular monitor the Sun in order to give early warning of coronal mass ejections (CMEs).

       How early? Well hopefully days, but maybe sometime only hours (see Wikipedia: Coronal mass ejection: Physical Properties). Early warning is particularly necessary for super coronal mass ejection (CMEs) (e.g., the Solar storm of 1859 (AKA the Carrington event) and the May 1921 geomagnetic storm (AKA New York Railroad Storm of 1921)) which could burn out the electrical power grids worldwide which would be a major disaster. Simply breaking the electrical power grid connections for a few hours while a super CME passes over could prevent said major disaster.

    
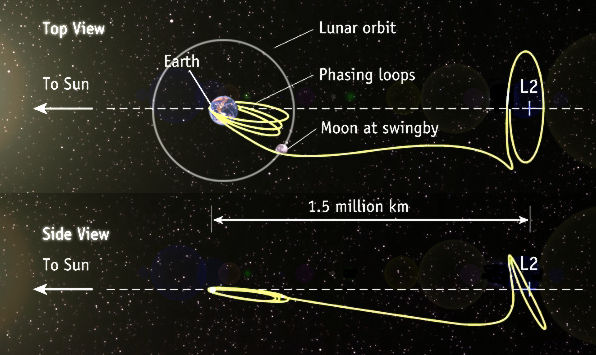
17. Image 3 Caption: "An xample of a Lissajous orbit around Sun-Earth Lagrange L2 point." (Slightly edited.)
18. Image 4 Caption: "An animation trajectory - Viewd from Earth Wilkinson Microwave Anisotropy Probe (WMAP, 2001--2010) trajectory as seen from Earth." (Slightly edited.) WMAP (2001--2010) went into Lissajous orbit around Sun-Earth Lagrange L2 point.

Images:

1. Credit/Permission: © User:Anynobody, 2009 / Creative Commons CC BY-SA 3.0.
   Image link: Wikimedia Commons: File:Lagrangianpointsanimated.gif.
   
2. Credit/Permission: © User:Cmglee, 2013 / CC BY-SA 3.0.
   Image link: Wikimedia Commons.
   
3. Credit/Permission: User:Abestrobi, 2009 / Public domain.
   Image link: Wikimedia Commons: File:Lissajous orbit l2.jpg.
   
4. Credit/Permission: © User:Phoenix7777, 2018 CC BY-SA 4.0.
   Image link: Wikimedia Commons: File:Animation of Wilkinson Microwave Anisotropy Probe trajectory - Viewd from Earth.gif.