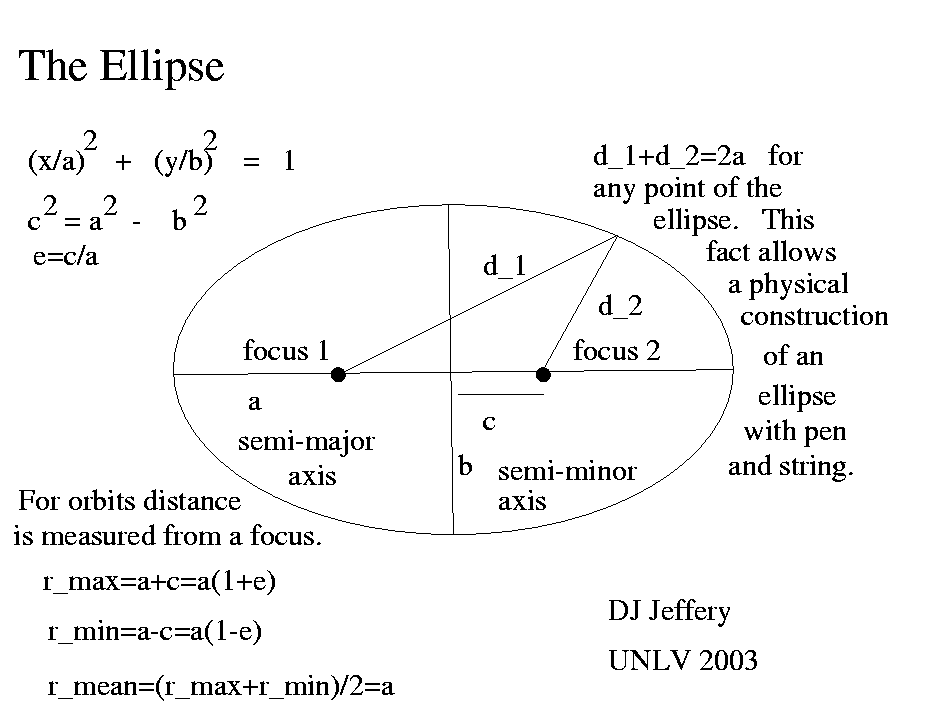
An ellipse is a closed geometrical curve of which the circle is a
special case. The Cartesian plane formula for a circle is
x2+y2=r2 ,
where r is the radius. The ellipse formula is
(x/a)2+(y/b)2=1 ,
where a and b are, respectively, the semi-major and semi-minor
axes (a > b asssumed without loss of generality). If a = b, then the ellipse is circle of
radius a.
The figure to the right shows an ellipse with its foci and accompanying
formulae.
A string fixed at two points and held taut with a pen then the pen can be
used to trace an ellipse with the two points becoming the foci: the
semi-major axis half the string's length.
For astronomical orbital purposes, it turns out that the physically important distance is from one focus to the curve, and not from the geometric center to the curve.
The eccentricity e of an ellipse (which defined mathematically on the figure above) is loosely speaking a measure of the DEVIATION of the ellipse from circularity. If e = 0, the ellipse is a circle. If e = 4/5, the ellipse is quite quite elliptical: the semi-minor to semi-major axis ratio is 3/5. If the semi-minor to semi-major axis ratio is 1/10, the e = 0.995 approximately. If e = 1, then the ellipse has flattened into a line segment if one sends semi-minor axis b to zero and holds the semi-major a axis constant. (You get different answer for e = 1, when you allow a and b to go to infinity in just the right way.)
The figure below illustrates how eccentricity affects ellipse shape.
Beyond the scope of intro astro, there are more at site Ellipse Arcana.
-
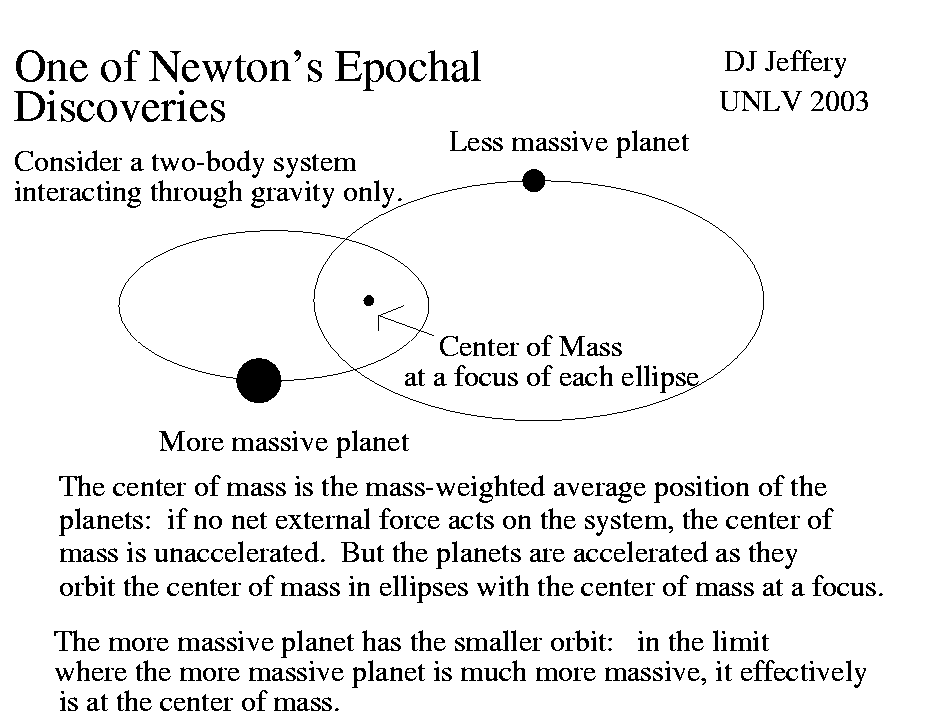
One of Isaac Newton's (1643--1727)
epochal discoveries was that two bodies that
treated as point masses, isolated from all other bodies
in space, will orbit their mutual
center of mass
(called the barycenter
for orbits)
in ellipses
where the center of mass is at one of the focuses of
each of the ellipses:
the other focus in each ellipse is just an empty point in space---the
center of mass can be just an empty point too, of course.
The situation is illustrated in the figure below.
Of course, one means "orbit the center of mass" in a physical sense:
i.e., the center of mass
defines
inertial frame
which means in modern understanding the
center of mass
is in free fall
in sufficiently uniform external
gravitational field.
The BODIES ARE ACCELERATED since they are NOT in uniform straight line motion relative to the inertial frame of the center of mass. There is an internal force causing them to move in orbit.
That internal force is, of course, GRAVITY. Elliptical orbits are a consequence of the INVERSE-SQUARE LAW of Newton's law of universal gravitation which was itself another epochal discovery of Newton.
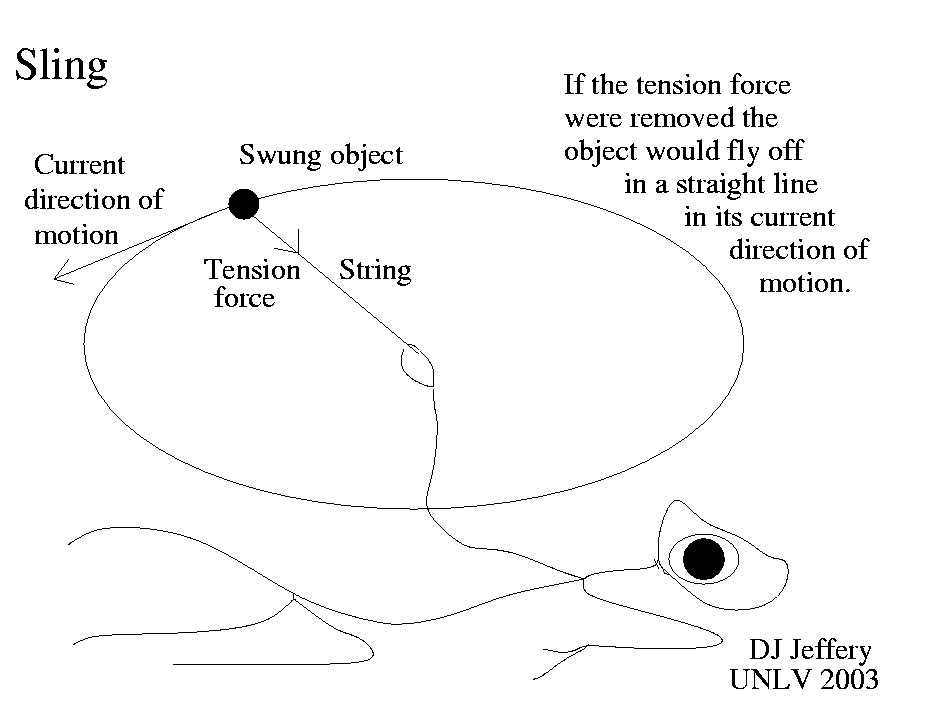
Another example of "orbiting' is the circular motion of a SWIRLED SLING: see the figure below. Here the center of force is relatively unmoving (unaccelerated) hand and the swung object is accelerated by the TENSION force of the string into circular motion. If the tension force vanished, the object would fly off in a straight line if not acted on by gravity. Of course, with a sling the flying off is the whole point.
How is it that the
Sun
and each planet
individtually can be approximated to 1st order as a
gravitational two-body system?
The figure below gives the explication.
-
Part of
astro-jargon
are special names for the points of closest and farthest approach
for 2 bodies in a
2-body system:
periapsis
and
apoapsis.
Note that peri
means something like around, apo something like off:
both fragments are derived from
Greek.
- In general: periapsis and apoapsis.
- For the Earth: perigee and apogee. Note gee means Earth and is derived from Greek.
- For the Sun: perihelion and aphelion.
- For Jupiter: perijove and apojove.
- For a star: periastron and apastron.
- etc.
Periapsis and apoapsis are the general terms. There are special case ones for special 2-body systems:
The SPEED OF A BODY in orbit varies. It is faster when nearer to the center of force and slower when farther from the center of force. The highest speed is at periapsis and the lowest at apoapsis .
-
The figure below illustrates orbits
with terminology for a
planet
in the
Solar System.
The
Table: Solar-System Planets
below gives, among other things,
planet mean distances (from the Sun), eccentricities, and ecliptic angles.
Don't try to memorize these numbers: look at them and think
about what they mean.
As the
Table: Solar-System Planets
shows, the PLANET ORBITS are close to CIRCULAR:
i.e., the eccentricities are small.
For example consider the Earth's eccentricity of 0.0167.
This means that the Earth is only ever 1.67 % farther from the
Sun that its mean distance and only 1.67 % closer to the Sun
than its mean distance.
Venus has the smallest eccentricity.
Thinking of the planet orbits as CIRCULAR is a fine first order approximation. But for detailed predictions one must go to ELLIPTICAL ORBITS and even further to PERTURBED ELLIPTICAL ORBITS. Detailed prediction of angular position on the sky has always been one of the goals of astronomy since ancient times. In fact ASTRONOMICAL ACCURACY is a byword.
Alas, ASTROPHYSICAL ACCURACY is a byword too: sympathetically
it means order of magnitude accuracy; unsympathetically it
means "we don't know what were talking about."
The ECLIPTIC ANGLE is the angle inclination of the plane of the orbit from ecliptic plane (i.e., the plane of the Earth's orbit). We see that the planets nearly orbit all in the same plane. Pluto and Mercury have the two largest inclinations by far as illustrated in the figure below. The asteroids orbits are close to the ecliptic too. However, long-period comet orbits can be at any angle relative to the ecliptic.