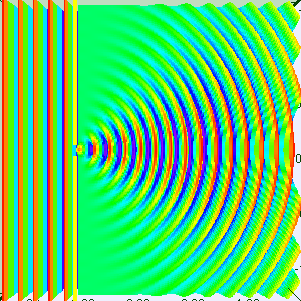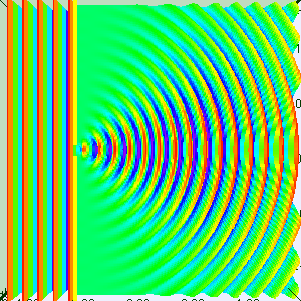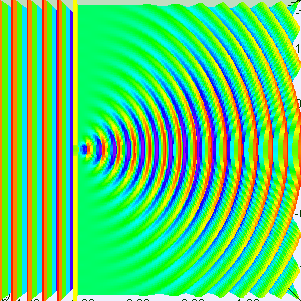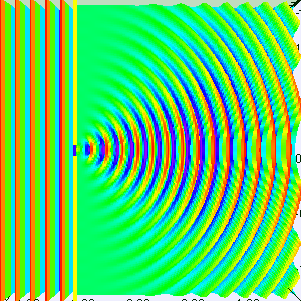
Caption: Two animations showing the diffraction of plane waves through apertures of width w_aperture. The first with R = λ/w_aperture = 1/5 and the second R = λ/w_aperture = 1/1.

Features:

1. In the animations red and dark blue represent the oscillations in high intensity waves.

   Green and faint blue represent the oscillations in low intensity waves.

2. The apertures in the animations are probably long slits that we see in cross section

   The caption with the animations is mute on this point.

3. Diffraction of waves through an aperture or around an obstactle scales as R = λ/w_scale, where w_scale is a characteristic size for the aperture/obstacle.

   

4. If R << 1, then diffraction pattern is mostly weak.

   It is still present, but has very low intensity, except for the central bright fringe. The other fringes, bright and dark, become very narrow.

   The central bright fringe approaches being beam-like as if it were just made up of rays executing rectilinear propagation.

5. Optics in the realm of R << 1 is called geometrical optics. In geometrical optics, light is treated as consisting of light rays and the wave nature of light is NOT directly manifested.

   In most everyday life situations with human-scale apertures and obstacles, geometrical optics describes the behavior of light to high accuracy.

   In fact, the wave nature of light is seldom noticed.

6. The first animation illustrates case of R = λ/w_aperture = 1/5, where w_aperture is the w_scale in this case.

   Here the R is significantly less than 1, but most would probably NOT consider R << 1.

   Nevertheless, the central bright fringe is strong and rather beam-like and the other fringes are narrow and faint.

   If R were made very small, the central bright fringe would become like a straight rectangular beam and the rest of the diffraction pattern would become very faint with narrow fringes visible just near the edges of the central bright fringe.

7. If R ∼1 or R > 1, the diffraction pattern becomes obvious.

8. This case is what we see in the second animation where R = 1.

   Here the central bright fringe broadens instead of becoming a beam as when R becomes small.

   The off-axis intensity of the diffraction pattern is increased relative to the first animation.

9. If R → ∞, then the central bright fringe would become a hemispherical wave pattern as from a point light source on an opaque wall.

Images:

1. Image link: Wikimedia Commons: File:5wavelength=slitwidthsprectrum.gif.
   
2. Image link: Wikimedia Commons: File:Wavelength=slitwidthspectrum.gif.