UNDER RECONSTRUCTION BELOW and maybe just cannibalization

General Caption: It is difficult to be correct, concise, and comprehensible about inertial frames. But they are very important, and so an understanding is necessary.

Sections:

Space:
Space does have a physical nature that affects the interactions between all objects and particles including the massless particles (e.g., the photon). On the relatively small scale (i.e., much smaller than the observable universe) that physical nature is manifested by inertial frames in the sense that all physical theories (or physical laws if you like) are referenced to inertial frames (at least in their basic formulation), except general relativity which tells us what inertial frames are.
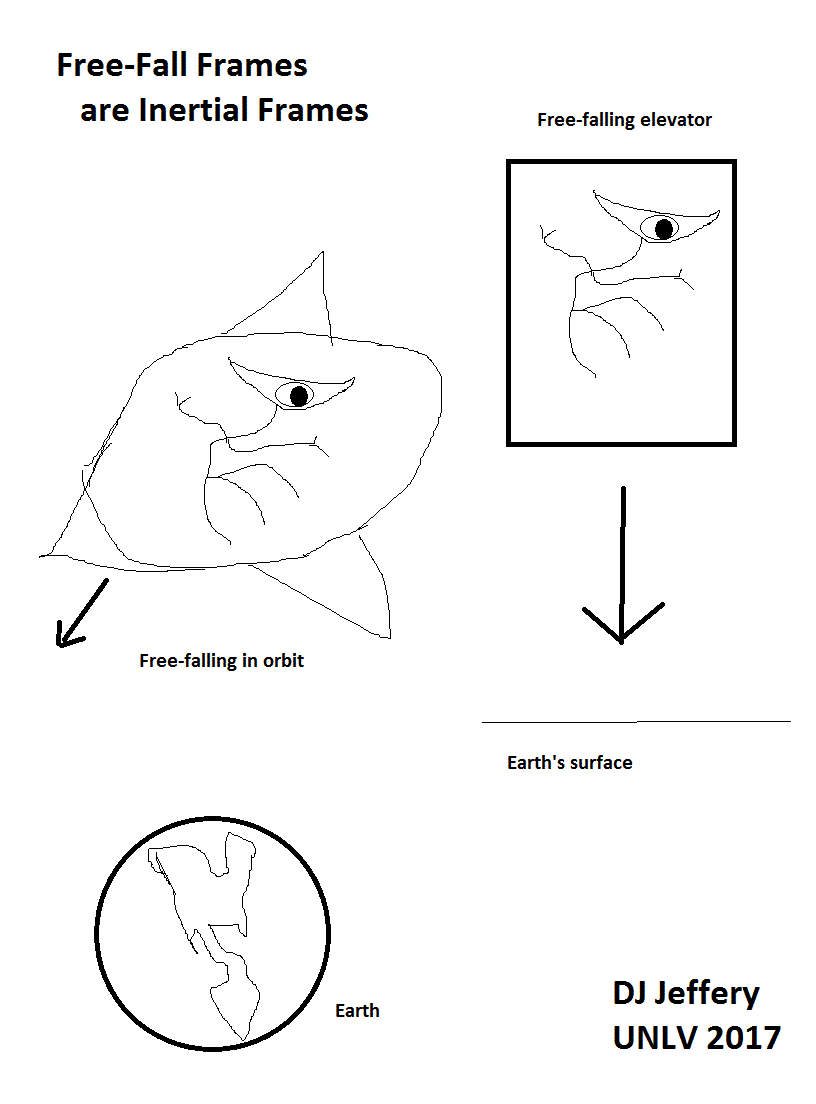
Image 1 Caption:
Free-fall frames are inertial frames. The spacecraft and free-falling elevator are elementary inertial frames in the jargon introduced below in section The Elementary Inertial Frame. The Earth's center of mass is the origin of the CMIF system consisting of the Earth alone in the jargon introduced below in section CM Inertial Frame (CMIF) Systems.
The Elementary Inertial Frame:
1. The elementary inertial frame (a nonce name) is a simple free-fall frame.
  To be concrete, consider a spacecraft free-falling in space: it is just moving under the gravitational force of the local external gravitational field (i.e., the gravitational field of the rest of the universe). The spacecraft is small enough that the external gravitational field is uniform over the whole spacecraft and the spacecraft's self-gravity is negligible.
2. Attach a coordinate system to the center of mass of the spacecraft. The coordinate system is NOT rotating with respect to the observable universe (which is a shorthand for with respect to the bulk mass-energy of the observable universe).
  All physical theories (valid ones that is) referenced to the coordinate system yield the exactly the right behavior to within experimental error as far as we know. An important example is Newtonian physics which holds in the classical limit.
  The coordinate system specifies an elementary inertial frame.
3. Albert Einstein (1879--1955) argued for the statements above (using an elevator rather than a spacecraft) and summarized them in the Einstein equivalence principle (which is usually strengthened to the strong equivalence principle) which is a basic principle or axiom of general relativity.
  Nowadays general relativity is fairly well confirmed theory and that confirms the strong equivalence principle and the concept of an elementary inertial frame.
  It seems likely that even if general relativity turns out to be wrong (i.e., NOT a valid emergent theory) that the concept of an elementary inertial frame will still be true---because it is experimentally verified in its own right to pretty high accuracy/precision.
Comoving Frames:
1. Modern cosmology (which is based on general relativity among many other things) tells us there are a special set of elementary inertial frames. These frames participate in the mean expansion of the universe and are called comoving frames.
2. The expansion of the universe is dictated Friedmann equations which are derived using general relativity and other assumptions including the cosmological principle (which states the universe is homogeneous and isotropic on a sufficiently large scale of order 100 Mpc: see Wikipedia: Cosmological principle: Observations).
  The expansion of the universe is, in fact, just an overall scaling up of the distances between gravitationally bound systems. The systems and their contents do NOT expand.
3. The Friedmann equations can actually be derived from Newtonian physics plus extra hypotheses NOT in pure Newtonian physics. We can call this the semi-Newtonian derivation.
  The semi-Newtonian derivation does derive comoving frames using inertial frames (i.e., reference frame in which Newtonian physics holds) and shows that comoving frames are inertial frames.
4. The Friedmann-equation (FE) models are the solutions of the Friedmann equations and are are the actual cosmological models.
  FE models tells us how the comoving frames move with respect to each other: i.e., their relative velocities and accelerations and that their separations just grow with the scaling up of the universe.
5. Actually, the FE models generalize the concept of elementary inertial frame in the sense that free fall is NOT just under gravity, but also under the effect of cosmological constant (AKA Lambda, Λ) and/or dark energy. The cosmological constant and/or dark energy are the hypothetical causes of the observed acceleration of the expansion of the universe.
CM Inertial Frame (CMIF) Systems:
1. The center of mass (CM) of any system of astro-bodies (which system could consist of just one astro-bodies) that does NOT interact significantly with respect to any other local system (meaning in virtually all cases by gravity) moves with a comoving frame. Note the motion with the comoving frame is due to the gravity of the non-local mass-energy (i.e., the overall cosmological model) plus other overall effects (e.g., cosmological constant Λ and/or dark energy).
  This CM plus a coordinate system NOT rotating with respect to the observable universe defines what we can call a CM inertial frame (a nonce name). The system that defines the CM inertial frame, we will call a comoving frame CM inertial frame (CMIF) system (a nonce name).
  Important comoving frame CMIF systems are galaxy clusters, galaxy superclusters, and field galaxies (i.e., galaxies NOT in galaxy clusters).
2. The CM of any subsystem of astro-bodies of a comoving-frame CMIF system plus a coordinate system NOT rotating with respect to the observable universe also defines CM inertial frame The subsystem itself is a CMIF system without qualification.
  Virtually all recognized/named/natural systems of astro-bodies are CMIF systems: e.g.,
  Obviously, the CMIF systems form whole hierarchies: e.g., moon systems in planetary systems in star clusters in galaxies in galaxy clusters in galaxy superclusters.
3. Almost all the internal motions of a CMIF system can be analyzed using Newtonian physics as long as the CMIF system overall is in the classical limit (i.e., close enough for one's purposes to the classical limit):
  1. Relative velocities much less than the vacuum light speed c = 2.99792458*10**5 km/s.
  2. Gravitational fields much weaker than near black holes.
  3. Total mass-energy of the astro-body much less than that of the observable universe.
  4. The Size scale of the whole CMIF system is less than a typical galaxy supercluster. Galaxy superclusters are sufficiently large that they partially participate in the expansion of the universe which requires general relativity for its analysis.
  5. Size scale in the analysis much larger than the size scale of atoms and molecules.
  The classical limit sounds very restrictive, but pretty much everything from cosmic dust to galaxy clusters can be analyzed as in the classical limit in good to excellent approximation. The internal and nearby behavior of black holes CANNOT be so analyzed, of course.
4. The form of the Newton's 2nd law of motion (AKA F=ma) that applies to CMIF system (in the classical limit) is what we will call the CMIF 2nd law (a nonce name). From a derivation (using Newtonian physics and the understanding of comoving frames from the FE models) given in frame_inertial_free_fall_supplement.html, we obtain the CMIF 2nd law
```
  sum_j(F_ji/m_i) + gt_i = a_i  , where subscripts i and j label "particles" of the system
                                      i.e., objects where you can neglect the internal structure
                                      for the analysis you are doing,

        m_i is the mass of particle i,

        F, g (see below), gt, and a with appropriate adornments are vectors,

        F_ji is the force of particle j on particle i.  
            It includes gravity and any other forces.

        a_i is the acceleration of particle i relative to the
            the CM inertial frame,

        and gt_i is the tidal field (tidal force per unit mass) on particle i.

  gt_i = (g_i - g_ave) = [ (g_i-g) - sum_j[(m_j)*(g_j-g)/m] ] , where

        g_i is the external gravitational field on particle i:
            i.e., the gravitational field due to the
            rest of comoving frame CMIF system that contains the CMIF system 
            under consideration.
            If the CMIF system under consideration is the 
            whole comoving frame CMIF system
            then all g_i = 0 by our definition of
            comoving frame CMIF systems (see above),

        g_ave = sum_j(m_j*g_j)/m is average gravitational field,

        g is gravitational field at the center of mass, 

        and m =sum_j(m_j) is the total mass of the CM inertial frame system under consideration.  
```
  The CMIF 2nd law only allows us to solve for the motions of the particles making up the CMIF system. Other motions if needed (e.g., to provide the behavior of the tidal field gt_i) must be known by other means.
5. The Acceleration of the Center of Mass of a CMIF System:
  From the derivation given in frame_inertial_free_fall_supplement.html of the CMIF 2nd law, we also obtain Newton's 2nd law of motion (AKA F=ma) for the center of mass of the CMIF system:
```
          g_ave = sum_j(m_j*g_j)/m = a_cm  , 
```
  where a_cm is the acceleration relative the center of mass of the comoving frame CMIF system containing the CMIF system under consideration. Recall from section Comoving Frames, that comoving frames are inertial frames.
  Three further points:
  1. The g_i must in principle be calculated from all the mass-energy of the comoving frame CMIF system. The gravitational field from beyond the comoving frame CMIF system (as we assumed above in section CM Inertial Frame (CMIF) Systems) has NO effect in the comoving frame CMIF system other than in establishing the comoving frame itself.
    Because there is finite mass-energy of the comoving frame CMIF system, the g_i can be calculated. In fact, if there are gravity sources in many directions, there will be a lot of cancellation and sometimes only the relatively nearby sources may be needed for the calculation. However, recall the strength of gravity decreases relatively slowly as 1/r**2 according to inverse-square law where r is the distance to the source. So sometimes one might need to add contributions from fairly remote sources.
    But note that one does NOT need to calculate the g_i or g_ave in order to use CMIF 2nd law as we discuss just below in section The Tidal Field gt.
  2. In deriving the the CMIF 2nd law, -a_cm got substituted in the CMIF 2nd law in the form of -g_ave. The -a_cm in physics jargon is an inertial field (i.e., an inertial force per unit mass).
    Inertial forces are NOT ordinary forces since they are due to accelerations. But inertial field act just like the gravitational field in the reference frame in which they are used: i.e., they are linearly mass-dependent body forces. They act just like in all respects. This is the point of Einstein equivalence principle (usually strengthened to strong equivalence principle) and this implies that gravity is fundamentally an inertial force and NOT an ordinary force.
  3. Because of the last point, yours truly (probably just following a herd) believes the distinction between inertial frame and non-inertial frame is NOT fundamental, but relative or of perspective.
    Viewed from the "inside" a CMIF system is in an inertial frame and viewed from the outside (i.e., viewed outside) is in a non-inertial frame, unless the outside perspective just happens NOT to be in acceleration with respect to the center of mass of the CMIF system.
6. The Tidal Field gt:
  We need to expand on two points about the tidal field gt_i
  1. The tidal field gt_i (as seen from the second form of formula for gt_i) depends only differences in the external gravitational field between the location of the particles i making up the CMIF system and its center of mass. Differences in external gravitational field between two points separated by distance d decreases asymptotically as (d/r)**3 where r is the mean distance from the two points and the source of the gravitational field (see Wikipedia: Tidal force: Formulation). The (d/r)**3 decrease is much faster decrease than the inverse-square law 1/r**2 decrease of the external gravitational field itself. Thus, the tidal field is usually much easier to calculate than external gravitational field itself since one does NOT need to add contributions from so far from the CMIF system as for the external gravitational field itself. In many cases, the tidal field gt_i may be negligible as it is by definition for the elementary inertial frame.
  2. The second term in the second formulation of the tidal field gt_i may often be small due cancellation if the CMIF system and the external gravitational field have high symmetry. In fact, for the ideal Earth ocean tides, the second term is zero by cancellation (see earth_tide_ideal.html). The ideal Earth ocean tide behavior is the main behavior of the Earth ocean tides: all other behaviors are perturbations, but striking ones on the human scale.
Special Cases of the CMIF 2nd Law:
A couple of special cases of CMIF 2nd law are enlightening:
1. If the tidal field gt_i and the self-gravity of the CMIF system are negligible, then the CMIF 2nd law reduces to
```
 
  sum_j(F_ji/m_i) = a_i  , where the F_ji have no gravity component. 
          
```
  In this case, the CMIF system is an elementary inertial frame system.
2. If the tidal field gt_i is negligible and the CMIF system consists of only two spherically symmetric astro-bodies, then the CMIF 2nd law applied to the two astro-bodies gives
```
  F_21/m_1 = a_1                for particle 1,  

  F_12/m_2 = a_2                for particle 2, 

  F_12/m_2 - F_21/m_1 = a_rel   for particle 2 relative to particle 1 with a_rel = a_2 - a_1,

  F_12(1/m_2 + 1/m_1) = a_rel   using Newton's 3rd law

  F_12 = m*a_rel  using the reduced mass formula m=(m_1*m_2)/(m_1+m_2).  
```
  The last formula can be used to solve the motion of particle 2 relative to particle 1 exactly. The overall solution for both particles can then be found exactly. This solution is famous exact 2-body solution of Newtonian physics. It's very useful since many systems approximate the 2-body solution system: e.g., the Sun and each Solar System planet individually.
3. General Inertial Frames:
  1. Spacecraft have their uses, but physics does have to deal with bigger systems---moons, planets, stars, galaxies, observable universe, etc. So inertial frames more general than the elementary inertial frame would be useful and they do exist.
    Consider an system of astronomical objects (which system could consist of just one astronomical object) that is affected significanly by the rest of the universe only via the external gravitational field (i.e, the gravitational field due to the rest of the universe).
    ????
  2. All the internal motions of the astro-body can be analyzed in this CM inertial frame using Newtonian physics as long as the astro-body is in the classical limit:
    1. Relative velocities much less than the vacuum light speed c = 2.99792458*10**5 km/s.
    2. Gravitational field much less than near black holes.
    3. Total mass-energy of the astro-body much less than that of the observable universe.
    4. Size scale in the analysis much larger than the size scale of atoms and molecules.
    The classical limit sounds very restrictive, but pretty much everything from cosmic dust to the large scale structure can be analyzed as in the classical limit in good to excellent approximation. Black holes CANNOT of course.
Image 2 Caption: A view from the south celestial pole (SCP) side of the celestial sphere, and so the orbital motions and rotational motions are clockwise.

Images:

Credit/Permission: © David Jeffery, 2017 / Own work.
Image link: Itself.
Credit/Permission: © User:Anynobody~commonswiki, 2011 / CC BY-SA 3.0.

local link: frame_inertial_free_fall_cef.html

.
File:

Mechanics file

frame_inertial_free_fall_cef.html