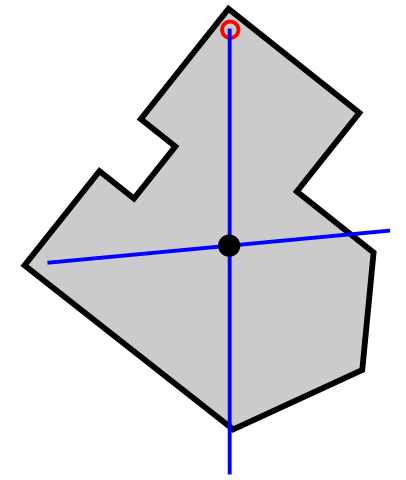
Caption: The center of mass of a rigid object can be found the hanging method as illustrated in the image.

Features:

1. You hang the object from two free pivots successively. In both cases, you allow the object to come to rest due to a small amount of friction at the pivot points.

   The red dot in the image represents a free pivot.

2. Each of the two hangings is a stable equilibrium: i.e., small perturbations from rest cause damped harmonic motion that asymptotically goes effectively to rest rather quickly.

3. Analysis by classical mechanics shows that the stable equilibrium has the object's center of mass lying directly below the pivot.

   Only with this location for the center of mass is the gravitational torque on the object Zorro---er, zero.

4. So lines drawn mentally straight downward from the two free pivots when each is used for hanging cross at the center of mass which is then located---neat, eh?

   The blue lines in the image represent the mentally-drawn lines.

5. What if the center of mass is directly above the pivot?

   This is balancing case is an unstable equilibrium. Ideally, a vanishingly small perturbation causes the object to accelerate away from the unstable equilibrium and usually NOT return by itself.

   A little bit of friction in the pivot makes the unstable equilibrium a bit metastable so that it can resist sufficiently tiny perturbations.

6. What if center of mass is right at the pivot?

   This is neutral equilibrium. The object will stay at rest for any orientation it is put in.