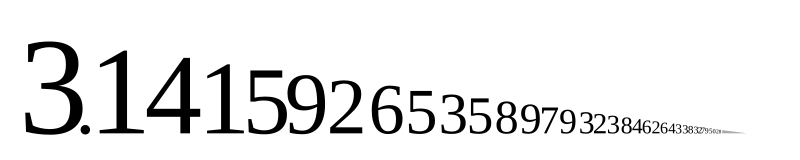
Caption: Pi constant = π = 3.1415 9265 3589 7932 38462 6433 ... illustrated.

π is the ratio of the circumference of a circle to its diameter (which is 2 times its radius): π=C/D=C/(2R).

π is an irrational number---it's mad, bad, and dangerous to know---like Lord Byron (1788--1824).

Which means it is NOT a rational number: it cannot be expressed as a ratio of integers, and so is incommensurable with integers.

Famous irrational numbers include:

1. The astronomical magnitude ratio = 100**(1/5) = 10**(2/5) = 2.511 8864 3150 95801 ... ≅ 2.512
2. The common logarithm of 2 = log(2) = 0.3010 2999 5663 981 ... ≅ 0.301
3. e = 2.71828 18284 59045 23536 02874 71352 66249 77572 47093 69995 ... ≅ 2.718
4. The Euler-Mascheroni constant γ = 0.57721 56649 01532 86060 65120 90082 40243 10421 59335 93992 ... ≅ 0.5772
5. The natural logarithm of 2 = ln(2) = 0.6931 47180 5599 45309 4172 32121 ... ≅ 0.6931
6. Pi = π = 3.1415 9265 3589 7932 38462 6433 ... ≅ 03.1416
7. The square root of 2 = √2 = 1.41421 35623 73095 0488 ... ≅ 1.414

Commensurable and incommensurable explicated:

1. Commensurable referring to a set of numbers just means that the numbers in the set have ratios that are rational numbers.

   Naturally, incommensurable means that a ratio is an irrational number.

2. In science, many sets of numbers, in particular those determined by experiment, are effectively incommensurable.

3. What does effectively incommensurable mean?

   Say you have a set of experimental measurements of continuous quantities (i.e., quantities that form continuum). You can only measure them to within experimental uncertainty.

   The quantities taken as exact values must be actually commensurable since each one is only known to a finite number of digits.

   But there are two difficulties with treating the values as commensurable

   First, if the number of digits is large for the values, then for practical purposes the values are incommensurable.

   With a large number of digits, the common unit for the values is probably tiny compared to the values and the values are probably NOT nice, round multiples of the unit.

   Second, since the values are NOT exactly known, you do CANNOT use them as exactly commensurable whether they are actually commensurable or NOT.

   Sometimes a theory will tell you if the true values are or are NOT commensurable. That knowledge may or may NOT be useful depending on the case and on whether the theory is true.

   The upshot is that in many cases you cannot use a set of experimental values as commensurable: they are effectively incommensurable.

   Of course, they might be approximately commensurable for some purposes.

4. An example of a set of effectively incommensurable experimental values are the time periods that go into predicting (terrestrial) eclipses.
   One consequence among others of the effective incommensurability, is that every longitude to some approximation eventually gets hit by a total solar eclipse.

   In addition to the two difficulties discussed above for sets of effectively incommensurable experimental values, one has the additional problem that the time periods evolve slowly due to astronomical perturbations in a chaotic evolution.
   For example, the solar day is currently increasing is increasing by 1.70(5)*10**(-3) seconds per century (see Wikipedia: Earth-Moon case).

   The upshot is that there is NO cycle of eclipses for highly accurate/precise eclipse predictions.

   Numerical calculation on a computer can do accurate/precise eclipse prediction to the past and future for thousands of years, but probably NOT millions of years ???? due the aforesaid astronomical perturbations in a chaotic evolution.

5. Let's do a simpler example, to further explicate.

   Say event A happens every 2 time units, event B every 3 time units, and event C every 5 time units, and all the events happen simultaneously a time zero which is the first all-events event.

   Because the time periods are commensurable, there will be an exact repeating cycle with the all-events event happening every repeat time of 2*3*5=30 time units which has each of the periods as divisor.

   But if event B happens every π time units, then after the first all-events event there will NEVER be another exact all-events event.

   To prove this, let's assume the contrary and show that there is a contradiction.

   Say the all-events event repeats. Then it must happen at a time 2*f=π*g=5*h, where f, h and g are integers.

   But this means that π=2*f/g which implies that π is a rational number.

   But π is a known to be an irrational number.

   So we have a contradiction. Thus, there is no repeat time for an all-events event.

   The set of time periods with event B having time period π is incommensurable.