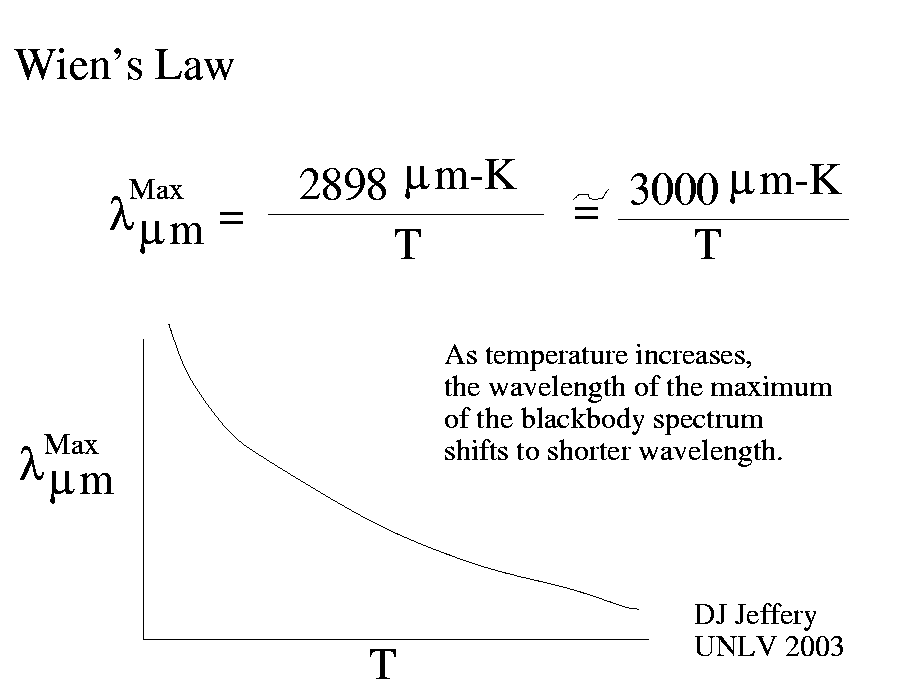
Caption: Wien's law illustrated.
Features:
- Wien's law is an exact result
for blackbody radiation.
It is a relationship between the temperature
of the blackbody radiator
and the peak of the blackbody spectrum.
-
The other famous simple blackbody radiation
law is the Stefan-Boltzmann law
that gives the
wavelength-integrated
flux of a
blackbody spectrum.
- Wien's law in terms of
general physical constants is
λ_max = (1/4.96511423 ...)*[hc/(kT)] ,
where h is the Planck constant h = 6.62607015*10**(-34) J·s = (4.135667696 ...) *10**(-15) eV·s (exact), c is the vacuum light speed c = 2.99792458*10**8 m/s = 2.99792458*10**5 km/s (exact) ≅ 3*10**5 km/s, k is the Boltzmann contant k = 1.380649*10**(-23) J/K = 8.617333262 ... )*10**(-5) eV/K (exact) ≅ 10**(-4) eV/K, T is the Kelvin temperature of the radiating body, and the coefficient (1/4.96511423 ...) is a dimensionless number (it is an irrational number) that follows from the derivation of Wien's law from Planck's law). For reference, see also NIST: Fundamental Physical Constants. - Wien's law is
an inverse relationship: as temperature
rises, the maximizing wavelength decreases.
In shorthand: T ↑ λ_max ↓.
- Note that wavelength goes to infinity if
temperature goes to zero.
This indeterminate result is rendered harmless by the fact that at
T = 0 K (which is absolute zero),
there is no blackbody radiation emitted.
We know this from
the Stefan-Boltzmann law.
- Wien's law and its inverse
(which can also be called Wien's law
or the inverse Wien's law)
in terms of fiducial values are, respectively,
2897.771955 ... μm·K 2897.771955 ... Å·K λ_max = -------------------- = ------------------- T T/10**4 and 2897.771955 ... μm·K (2897.771955 ...)*10**4 Å·K T = -------------------- = --------------------------- , λ_max λ_maxwhere wavelength λ_max is in microns (μm) for the first versions and angstroms (Å) for the second versions, and the Wien's law constant (with ellipsis ... to show the value is an exact irrational number) is from CODATA: Fundamental Physical Constants --- Complete Listing.Compact forms are Wien's law λ_max = 2897.7729(17) μm·K/T = 2.8977729(17) Å·K/(T/10**7) = (1/4.96511423 ...)*(hc/k)/T and Wien's law inverse T = 2897.7729(17) μm·K/λ_max = 2.8977729(17)*10**7 Å·K/λ_max.
- A temperature obtained
by an application of
the inverse Wien's law
to the peak of the
spectrum of
a general radiator (one NOT necessarily
a blackbody radiator)
is a color temperature.
-
Note that the general definition of
color temperature for a radiator
is the temperature
of a perfect blackbody radiator
that radiates
electromagnetic radiation (EMR)
with a spectrum
comparable in shape in some sense to that of said radiator.
- A color temperature
is a characteristic (i.e., rough average)
photospheric temperature
for stars.
However, the standard characteristic photospheric temperature is what is called the effective temperature. A discussion effective temperature and color temperature is given at Effective Temperature and Color Temperature.
Image link: Itself.
Local file: local link: wien_law.html.
File: Blackbody file: wien_law.html.