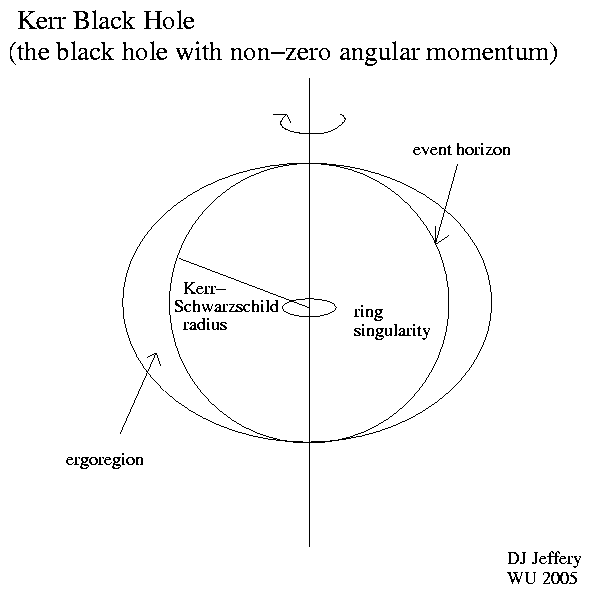
Caption: Cartoon of a Kerr black hole.

Features:

1. Kerr black holes follow from the Kerr solution to general relativity discovered by Roy Kerr (1934--).

   The Kerr solution is an exact analytic solution.

   Real Kerr black holes will NEVER match the exact ones (which are ideal limits) that follow from the Kerr solution because they are always subject to astronomical perturbations. This goes WITHOUT saying usually. But real Kerr black holes approximate ideal Kerr black holes well enough that one usually just says Kerr black holes WITHOUT qualification to mean real Kerr black holes.

   In fact, it is generally true in all empirical science that exact analytic solutions are ideal limits that reality only approaches more or less closely depending on the amount of perturbation. And this goes WITHOUT saying usually.

2. By the black-holes-have-no-hair theorem, ideal black holes have only 3 free parameters: mass, angular momentum, and net electric charge.

   Kerr black holes have mass and angular momentum, but zero net electric charge.

   The black-holes-have-no-hair theorem applies only to ideal, unperturbed black holes and it may NOT be absolutely true (see Wikipedia: No-hair theorem).

3. Most black holes probably closely approximate Kerr black holes since virtually all astronomical objects in the observable universe have angular momentum and usually very low net electric charge.

   Note that the more slowly rotating the Kerr black hole, the more closely it are approximates a Schwarzschild black hole and, in fact, to some degree all black holes can be approximated as Schwarzschild black holes.

   To reiterate with a bit of extention, there are always astronomical perturbations, and so the black holes can only ever approach the ideal behavior of Kerr black holes and Schwarzschild black holes.

4. If there are black holes with significant net electric charge (and angular momentum), they are Kerr-Newman black holes.

   It was once thought that Kerr-Newman black holes were unlikely to actually exist, but since circa 2015 their existence has become more of a possibility.

5. Ideal Kerr black holes have a ring singularity rather than a point singularity (an infinite density point mass) as do ideal Schwarzschild black holes.

   The ring singularity is an infinitely thin, infinite point mass ring of mass.

   Of course, neither kind of singularity is thought to exist since it is thought that quantum gravity must prevent collapse to singularities. But without an established quantum gravity theory, we do NOT have an established theory for what is the actual collapsed center of a black hole. But it probably has volume and might be an oblate spheroid or a toroid for a Kerr black hole.

6. The Kerr-Schwarzschild radius is the Kerr solution analogue of the Schwarzschild radius and defines the event horizon: a spherical region from which or within which light CANNOT escape to infinity.

   There is a formula for the Kerr-Schwarzschild radius which is a generalization of the one for the Schwarzschild radius---but it's beyond our scope.

7. A new feature of Kerr black holes relative to Schwarzschild black holes is the ergosphere (AKA ergoregion).

   The ergosphere touches the event horizon at the rotation axis and is an oblate spheroid (as in the figure) for relatively low angular momentum and is a sort of symmetrical pumpkin shape for relatively high angular momentum (see Wikipedia: Ergosphere).

8. What defines the ergosphere?

   Well, a Kerr black hole twists the spacetime around it, and so causes frame-dragging (AKA the Lense-Thirring effect).

   The ergosphere is defined as that region where the frame-dragging is so strong that NO test particle in the ergosphere can be held stationary with respect to an outside observer. But with sufficient energy, a test particle in the ergosphere can escape to infinity since it is above the event horizon.????

   Recall a test particle is an object sufficiently negligible in effect on the physical system external to itself that it does NOT affect said physical system. Among other things, a test particle has negligible mass-energy.

   An object of finite mass-energy can resist being dragged if it has sufficient mass-energy to perturb the Kerr black hole structure.

9. Because of the importance of Kerr black holes (real ones, NOT ideal ones) as being the ones that exist in nature, they are very important, but here we will go NO further in explicating them.