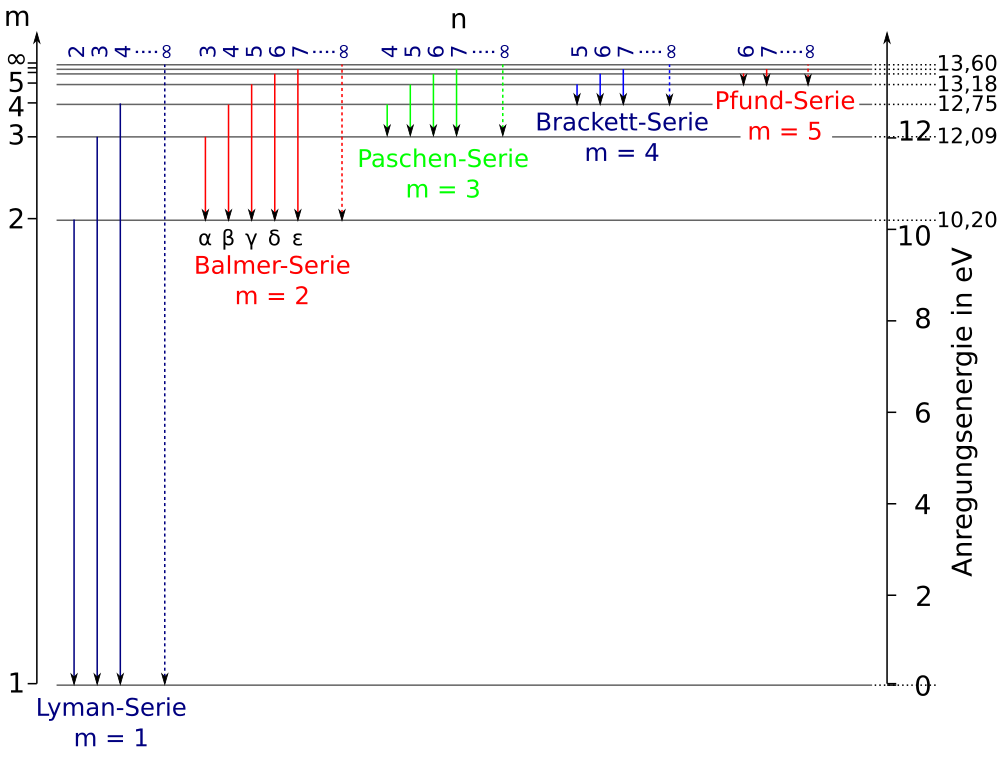
Caption: H I Grotrian diagram.

Features:

1. Grotrian diagrams are abstract diagrams of atoms and molecules. The vertical axis is the energy of the energy levels relative to the ground state (i.e., the lowest energy energy level). The energy unit here is, as is usually the case, the electron-volt (eV) which is the natural-unit energy unit for atomic and molecular energy levels. The horizontal axis distinguishes the energy levels by quantities other than energy (often various quantum numbers). Here the horizontal axis just distinguishes the atomic hydrogen line series: Lyman series, Balmer series, etc.

2. The Grotrian diagrams labels are in German. Just accept it.

3. H I is neutral hydrogen. H II is singly-ionized hydrogen which is just a bare proton and doesn't have any energy levels, and therefore doesn't have a Grotrian diagram.

4. The Grotrian diagram shows the energy levels and the atomic line transitions for the neutral hydrogen atom.

5. For energy levels, we use values for the ideal hydrogen atom (i.e., the hydrogen atom calculated without any perturbation corrections from quantum mechanics perturbation theory included, but using the correct reduced mass).

6. For atomic line transitions wavelengths, we use values tabulated by the National Institute of Science & Technnology (NIST) (formerly the National Bureau of Standards (NBS)) (Wiese et al. 1966, p. 2--4; Wiese et al. 1966, p. 2--4, online), except that we calculate the hydrogen series limit wavelengths from our energy levels using the de Broglie relation

     λ = hc/(E_n) = 1.23984197 μm/(-E_n) ≅ 1 μm/(-E_n)  .  

7. The formula for energies of the energy levels of the ideal hydrogen atom is

     E_n = -E_ryd*(μ/m_e)/n**2
   
         = -(13.5982 ... eV)/n**2  , 

   where the

   1. Rydberg energy = 13.60569253(30) eV,
   2. reduced Rydberg energy E_ryd = 13.5982 ... eV,
   3. electron reduced mass μ=m_e/(1+m_e/m_p)=(0.9994 ...)*m_e,
   4. electron rest-mass energy m_e=0.510998910(13) MeV,
   5. proton rest-mass energy m_p=938.272046(21) MeV, energy is in electron-volts (eV) (1 eV = 1.602176565(35)*10**(-19) joules = 10**(-6) MeV),
   6. n is the principal quantum number which runs 1, 2, 3, ... , ∞ in order of increasing energy level energy for the hydrogen atom.

   The zero point for the energies is zero energy of the continuum of energy states available to free (i.e., unbound) electrons.

8. To get the energy measured from the ground state of the hydrogen atom, one uses formula E_grd_n = E_n - E_1.

9. To get the energy of a particular transition, one uses the formula E = E_n_upper - E_n_lower.

10. In the table below, we show the hydrogen atom energy levels.

     ____________________________________________________
     Table:  Energy Levels of the Ideal Hydrogen Atom
     ____________________________________________________
       n      E_n           E_grd_n
              (eV)            (eV)
     ____________________________________________________
    
       1    -13.598 ...     0.0000 ...
       2    -3.3995 ...    10.1987 ...
       3    -1.5109 ...    12.0873 ...
       4    -0.8498 ...    12.7483 ...
       5    -0.5439 ...    13.0543 ...
       6    -0.3777 ...    13.2205 ...
       7    -0.2775 ...    13.3207 ...
       ∞     0             13.5982 ...
     ____________________________________________________ 

11. An important sample of the atomic line transitions for the hydrogen atom are tabulated below. The wavelengths are for air NOT vacuum.
    Table: Atomic Hydrogen Spectral Series:
    1. Lyman series n ≥ 2 → 1 transitions:
       1. Lyα n=2 → 1, λ=1.21567 μm, E=10.1987 ... eV
       2. Lyman limit n=∞ → 1, λ=0.91176 μm, E=13.5982 ... eV
    2. Balmer series n ≥ 3 → n=2 transitions:
       1. Hα n=3 → 2, λ=0.656280 μm, E=1.8886 ... eV
       2. Hβ n=4 → 2, λ=0.486132 μm, E=2.5496 ... eV
       3. Hγ n=5 → 2, λ=0.434046 μm, E=2.8556 ... eV
       4. Hδ n=6 → 2, λ=0.410173 μm, E=3.0218 ... eV
       5. Hε n=7 → 2, λ=0.397007 μm, E=3.1220 ... eV
       6. Balmer limit n=∞ → 2, λ=0.3647 μm, E=3.3995 ... eV
    3. Paschen series n ≥ 4 → 3 transitions:
       1. Paα n=4 → 3, λ=1.87510 μm, E=0.6610 ... eV
       2. Paschen limit n=∞ → 3, λ=0.8206 μm, E=1.5109 ... eV
    4. Brackett series n ≥ 5 → 4 transitions:
       1. Brα n=5 → 4, λ=4.05120 μm, E=0.3059 ... eV
       2. Paschen limit n=∞ → 4, λ=1.4588 μm, E=0.8498 ... eV
    5. Pfund series n ≥ 6 → 5 transitions:
       1. Pfα n=6 → 5, λ=7.4578 μm, E=0.1662 ... eV
       2. Pfund limit n=∞ → 5, λ= 2.2794 μm, E=0.5439 ... eV
    6. Humphreys series n ≥ 7 → 6 transitions:
       1. Huα n=7 → 6, λ=12.3680 μm, E=0.1002 ... eV
       2. Humphreys limit n=∞ → 5, λ= 3.2823 μm, E=0.3777 ... eV
    7. No name series n ≥ 8 → n ≥ 7 transitions

Credit/Permission: © User:Kiko2000, User:Cepheiden, 2000 / Creative Commons CC BY-SA 3.0.
Image link: Wikipedia: File:Wasserstoff-Termschema.svg.
Local file: local link: grotrian_01_00_H_I.html.
File: atomic/grotrian file: grotrian_01_00_H_I.html.