Image 1 Caption: Eratosthenes (c.276--c.195 BCE) (who lived and worked in Ptolemaic Egypt) measured the circumference---and thereby also radius---of the Earth. His menthod is illustrated in the 2 images.

1. Eratosthenes made the assumption of a spherical Earth. The ancient Greeks had been aware of the spherical Earth theory. since the theory was recorded (and perhaps discovered) by perhaps Parmenides (fl. c.500 BCE) (see, e.g., David Furley (1922--2010), The Greek Cosmologists, 1987, p. 41, 56). Strong empirical evidence for a spherical Earth was known by Eratosthenes' time and maybe since Parmenides. Perhaps NOT overwhelmingly convincing, but pretty convincing. For more on the spherical Earth theory in Greco-Roman antiquity, see parmenides_earth.html and Wikipedia: Spherical Earth: Antiquity.

2. Eratosthenes also assumed that the Sun was so remote that light rays from the Sun were parallel when they arrived at the Earth. No evidence contradicted this theory. Attempts to measure the Sun's distance were probably known to Eratosthenes and it was probably known that they were probably failures because the Sun was too remote for the techniques available then. Of the ancient Greek astronomers, it can be said their geometry was strong, but their instruments were weak.

   In fact, if the ancient Greek astronomers had the right idea of the heliocentric solar system model and put their minds to it they could have measured the Earth-Sun distance to fair accuracy just as was done in the 17th century by Jean Richer (1630--1696) and Giovanni Domenico Cassini (1625--1712) in 1672 (see Wikipedia: Astronomical unit: History). In fact moreover, if Eratosthenes (c.276--c.195 BCE), Archimedes (c.287--c.212 BCE) (arguably both greatest ancient Greek mathematician and experimentalist), Aristarchos of Samos (c.310--c.230 BCE) (the first heliocentric solar system), and Ktesibios (c.285--c.222 BCE) (another great experimentalist) had put their great brain together, they could have done it.

3. It was known to Eratosthenes that in Syene (now Aswan) (on the Nile in Egypt) that the Sun was at zenith at solar noon on the day of the summer solstice. This means that Syene is on the Tropic of Cancer. See Image 1.

   

4. At the same time in Alexandria---the city founded by Alexander the Great (356--323) which he named for himself---the Sun was 7° south of zenith along the meridian.

   Of Alexandros:

   ... coming into his own city Alexandria,
   he found no memory of his time,
   not even a stone set on stone,
   and he rested on a stone,
   for a moment.
   

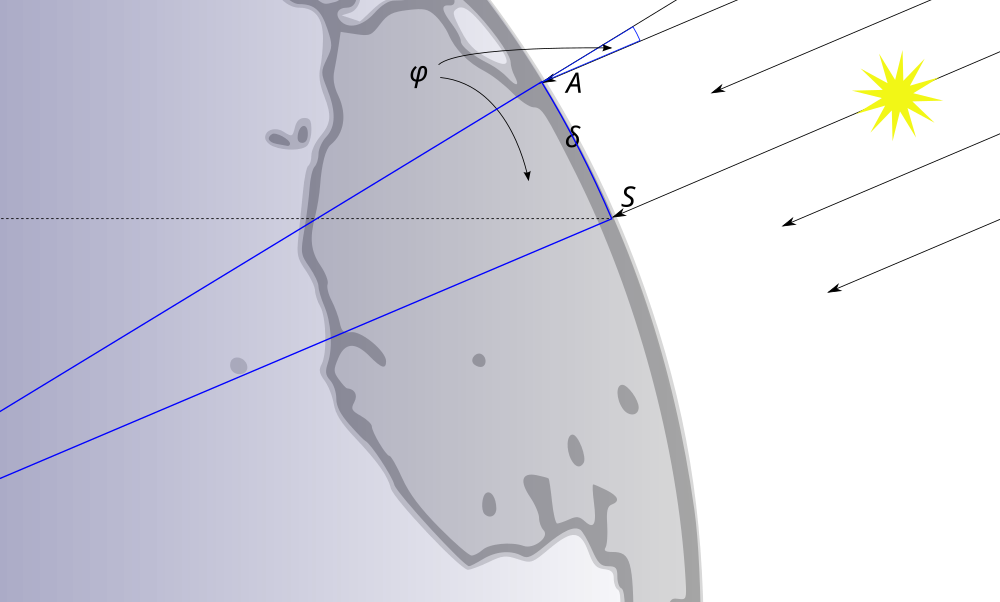
5. Image 2 Caption: Another diagram that helps make the geometical situation clear.

   The angle φ between the zenith direction in Alexandria and a light ray from the Sun is equal to the angle between the radius to Alexandria and the radius to Syene by the converse of Euclid's parallel postulate (see also Euclidean parallelism axiom). The radius to Alexandria is a transversal that intersects 2 parallel straight lines.

6. Behold:

     φ/360=S/C  ,  and so C = (360/φ)S = 50*5020 = 252000 stadia
   
     C = (252000 stadia) * [0.1577 km/(1 stadion)] ≅ 39700 km
   
     and
   
     r = C/(2π) ≅ 6320 km  .  

   where φ = 7.2° = 1/50 of a circle as measured by Eratosthenes, S is the arc length between Alexandria and Syene, C is the circumference of the Earth, and the Eratosthenian stadion = 0.1577 km (modern estimate).

7. Alas, we are NOT certain which station Eratosthenes used, but the Eratosthenian stadion, as we can call it for the nonce, is our best assumption. With that assumption, Eratosthenes' values are ∼ 0.7 % smaller than modern values for the Earth meridional circumference = 40007.86 km and the Earth mean radius R_me_⊕ = 6371.0088 km. This is really very good agreement for an ancient measurement.

8. By the by, recall that the Earth is NOT perfectly spherical.

Images:

1. Credit/Permission: © User:Cmglee, 2005 / Creative Commons CC BY-SA 4.0.
   Image link: Wikimedia Commons: File:Eratosthenes measure of Earth circumference.svg.
   
2. Image Credit/Permission: © User:Erzbischof, 2009 / Creative Commons CC BY-SA 3.0.
   Image link: Wikipedia: File:Eratosthenes.svg.