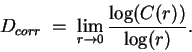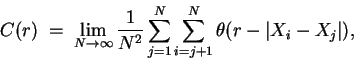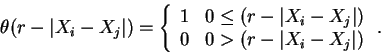Next: Calculating Fractal Dimension
Up: Defining Fractals and Fractal
Previous: Capacity Dimension
Correlation dimension can be calculated using the distances
between each pair of points in the set of N number of points,
A correlation function, C(r), is then calculated using,
C(r) has been found to follow a power law similar to the one seen in
the capacity dimension:
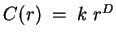 .
Therefore, we can find
Dcorr with estimation techniques derived from the formula:
.
Therefore, we can find
Dcorr with estimation techniques derived from the formula:
C(r) can be written in a more mathematical form as
where 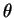 is the Heaviside step function described as,
is the Heaviside step function described as,
Sandip Thanki
1999-07-29