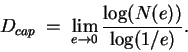Next: Correlation Dimension
Up: Defining Fractals and Fractal
Previous: Defining Fractals and Fractal
In order to find the capacity dimension of a set, we assume that the number
of elements covering a data set is inversely proportional to eD,
where e is the scale of covering elements and D is a constant. For
example, we have a line segment and we try to cover the segment
with squares of a certain size, and find that we need three
squares. If we then tried to see how many squares of half the original
size were required to cover the segment, it could be expected to have
six squares covering the segment, which is twice the number of squares
needed when the squares were at their original size. Thus, the number
of squares required to cover the segment is inversely proportional to
the size of the squares. The covering of any smooth, continuous curve
works the same way, provided that the size of the squares is small
enough so that the curve is approximated well by straight line
segments at that scale.
Thus, for one-dimensional objects, we see that
where e is the side of the square, N(e) is the
number of squares of that size required to cover the set, and kis some constant. Now suppose that we are covering a scrap of
paper with little squares. In this case, if we halve the size
of the squares, it would take four of the smaller squares to cover
what one of the larger squares would cover, and so we would
expect N(e) to increase by a factor of four when e is halved.
This is consistent with an equation of the form,
It seems reasonable to say that for more arbitrary sets,
where D is the dimension of the set. In other words, we can hope to
measure how much of two-dimensional space some subset of it comes
near by examining how efficiently the set can be covered by cells of
different size.
In order to find D from
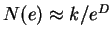 ,
we can solve the
formula for D, by taking the limit as
,
we can solve the
formula for D, by taking the limit as
 .
This is the capacity method of estimating D. If we further assume that
the set is scaled so that it fits into a square with side 1, then we get N(1)=k=1.
This yields the formula,
.
This is the capacity method of estimating D. If we further assume that
the set is scaled so that it fits into a square with side 1, then we get N(1)=k=1.
This yields the formula,




Next: Correlation Dimension
Up: Defining Fractals and Fractal
Previous: Defining Fractals and Fractal
Sandip Thanki
1999-07-29
![]() ,
we can solve the
formula for D, by taking the limit as
,
we can solve the
formula for D, by taking the limit as
![]() .
This is the capacity method of estimating D. If we further assume that
the set is scaled so that it fits into a square with side 1, then we get N(1)=k=1.
This yields the formula,
.
This is the capacity method of estimating D. If we further assume that
the set is scaled so that it fits into a square with side 1, then we get N(1)=k=1.
This yields the formula,