| Crystal Structure Prediction and its Application in Earth and Materials Sciences |
Before talking about the crystal structure, let us first consider the energy landscape for exploration. The number of distinct points on the landscape can be estimated as:
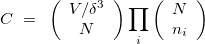 |
(1) |
where 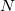 is the number of atoms in the unit cell of volume
is the number of atoms in the unit cell of volume 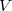 ,
, 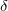 is a relevant discretization parameter (for instance, 1 ) and
is a relevant discretization parameter (for instance, 1 ) and  is the number of atoms of
is the number of atoms of  -th type in the unit cell. Even for small systems (
-th type in the unit cell. Even for small systems (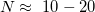 ),
), 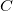 is astronomically large (roughly 10
is astronomically large (roughly 10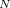 if one uses
if one uses 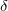 = 1 and typical atomic volume of 10
= 1 and typical atomic volume of 10  ).
).
The dimensionality of the energy landscape is:
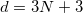 |
(2) |
where 3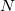 degrees of freedom are from
degrees of freedom are from 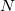 atoms, and the remaining six dimensions are defined by the lattice. At the first sight, CSP is basically a NP-hard problem, and the difficulty increases exponentially with the dimensionality. Yet, great simplification can be achieved if structures are relaxed, i.e. brought to the nearest local energy minima. Relaxation could introduce some intrinsic chemical constraints (bond length, bond angle). Therefore, the intrinsic dimensionality can be reduced:
atoms, and the remaining six dimensions are defined by the lattice. At the first sight, CSP is basically a NP-hard problem, and the difficulty increases exponentially with the dimensionality. Yet, great simplification can be achieved if structures are relaxed, i.e. brought to the nearest local energy minima. Relaxation could introduce some intrinsic chemical constraints (bond length, bond angle). Therefore, the intrinsic dimensionality can be reduced:
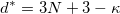 |
(3) |
where  is the number of correlated dimensions, which could vary a lot according to the intrinsic chemistry in the system. For example, the dimensionality drops a lot from 99 to 11.6 for Mg
is the number of correlated dimensions, which could vary a lot according to the intrinsic chemistry in the system. For example, the dimensionality drops a lot from 99 to 11.6 for Mg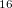 O
O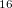 , while only a few from 39 to 32.5 for Mg
, while only a few from 39 to 32.5 for Mg N
N H
H . Thereby, the reduced complexity for the energy landscape of local minima is:
. Thereby, the reduced complexity for the energy landscape of local minima is:
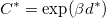 |
(4) |
![\includegraphics[scale=1.0]{pdf/landscape.png}](images/img-0024.png)
This implies that any efficient search method must include structure relaxation (local optimization). We also note that all the current global optimization methods must assume that the reduced landscape should have a overall shape (Fig. 2.1b) which could be optimized. Otherwise, for the extreme case like Golf-course like landscape (Fig. 2.1b), any global optimization methods would fail if the sampling space is not affordable.