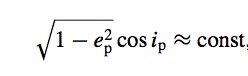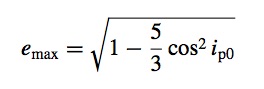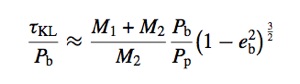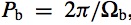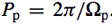We consider the orbit of a test particle around one component of a binary system. The Kozai-Lidov (KL) mechanism is important for orbits that are misaligned to the binary orbital plane by an angle greater than the critical KL angle (Kozai 1962, Lidov 1962). For a test particle, this is i=39 degrees. The KL mechanism periodically exchanges the particle’s inclination with its eccentricity.  During this process the component of the angular momentum that is perpendicular to the binary orbital planet is conserved. Thus,

where ep is the eccentricity and ip is the inclination of the particle. The maximum eccentricity that can be achieved is

(e.g. Innanen et al. 1997), where ip0 is the initial inclination.

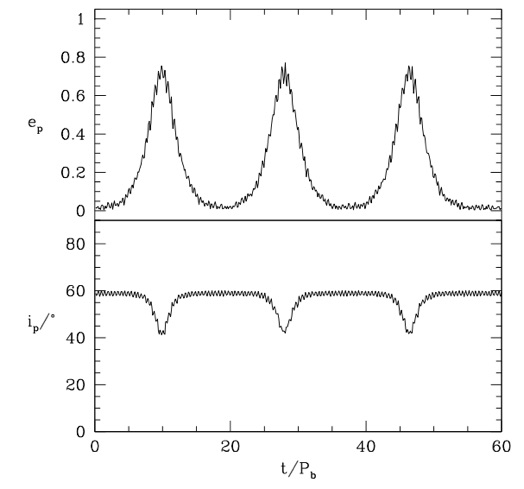
We first consider ballistic particle orbits around the primary of a circular orbit binary system. The primary has mass M1 and the secondary has mass M2 and they orbit at a separation, a. The total mass of the binary is M=M1+M2. The figure below shows the eccentricity and inclination evolution of a particle that has an initial distance of d = 0.2a from the primary and inclination of 60 degrees to the binary orbital plane.

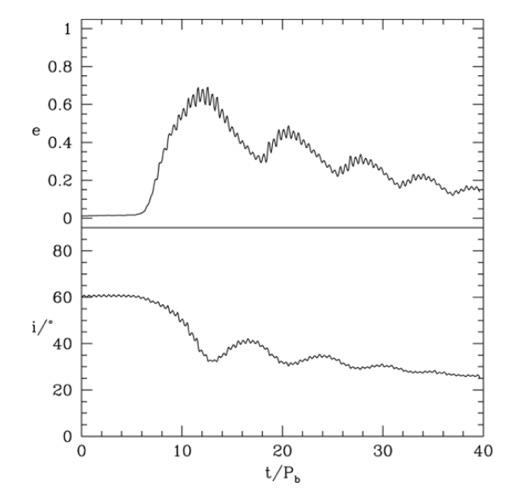
The analytic period for the KL oscillation timescale is

(e.g. Kiseleva et al. 1998), where the orbital period of the binary is

and the orbital period of the particle about the primary is                                       

In Martin et al. (2014) we found that a highly misaligned disc in a binary system is also unstable to global KL oscillations. The oscillations are are damped due to the dissipation within the disc and the disc eventually becomes circular and inclined at the critical KL angle.

These disc KL oscillations have important implications for accreting systems on all scales, for example, the formation of planets and satellites in circumstellar and circumplanetary discs, outbursts in X-ray binary systems and accretion on to supermassive black holes.