Imagine a time when proto-humans were wandering the planet. They are sitting huddled together, possibly in small groups, without fire, under the night sky.

Question 1: What might they have noticed about the night sky and Earth=s rhythms at the dawning of human consciousness?

Things in the sky: Stars, moon, planets, milky way, comets, meteors

Of course we cannot know when proto-humans became conscious of their surroundings in the sense that we are conscious of our surroundings, but obviously at some early time, humans or proto-humans, began to see patterns where no patterns had previously been observed. That transition undoubtedly happened, but when it happened lies outside of current human understanding.

Part of coming to grips with earth=s rhythms is developing a sense of time.

Question 2: How might a sense of time have developed in early humans? What units of time were the most natural to observe?

The day, the Amonth@, the year. How are they determined?

Sun=s motion B> Day

Moon=s motion B> week and month

Earth=s orbit of Sun B> seasons and year

Again it is hard to know how much of this Aawareness@ happened before our primate ancestors became modern humans, but clearly it happened before written records were kept, tens if not hundreds of thousands of years ago.

Observing the night sky, night after night, would have enabled ancient ancestors to notice important patterns.

The constancy of the night sky is the single most obvious thing. Our ancestors undoubtedly would have seen that the star patterns were constant. And just as undoubtedly, the natural way to recognize patterns was to use some sort of construct to help the mind sort out the various star patterns. For example, those five stars are called the Amammoth@ and those six the Atiger.@

Although the patterns were fixed, the locations of the patterns changed.

Question 4: How did the patterns move during the night and through the seasons?

Picture the rotation of the night sky. Through the fixed pattern of stars, the astute observer would have noticed objects that were not fixed as part of any particular star pattern but Awandered@ through the star patterns.

Question 5: What were these objects? How many were there?

Mercury, Venus, Mars, Saturn, and Jupiter.

The fixedness and consistency of the night sky are daunting. Consequently when something unexpected happened, a comet, a meteor, an eclipse, upset this consistency, it was easy to see those occurrences as Aomens.@

Two days after the Amoon was eaten by the tiger,@ Oona was trampled to death during the mammoth hunt. An incident like this would easily make our ancestors nervous about hunting mammoth after a lunar eclipse! (What is a lunar eclipse?)

Consequently, it seems natural that the night sky, and events in the night sky, would become associated with the daily happenings of humans. The more astute observers of both the night sky and human nature would become informal, at first, tribal seers, people to be consulted before going on a mammoth hunt or attacking a neighboring clan. As time passed, it seems plausible that some groups would want a more Aprofessional@ seer leading to the birth of astrologers, astronomers, and Aobservatories.@

As civilization developed, keeping track of time became more important.

Question 5: What development made dependable predicting the rhythmic change of seasons more important?

One obvious development was agriculture which needed accurate measurements of the year so that planting and harvesting could be done at the most opportune time. This meant that there were social and practical reasons to develop a good understanding of the rhythms of earth and their relationships to the night sky.

These observations were Areligious@ or Apractical.@

Around 300 to 400 BC Greek philosophers began to ask profoundly different sorts of questions. They began to apply logic and geometry to the heavens to find answers to questions that were probably never articulated before. Questions like: What is the shape of earth? How big is earth? How big is the moon? How big is sun? How far away is the moon? How far away is sun? These are astounding questions to ask let alone to answer.

The shape of earth: People begin to surmise that earth was a sphere because ships sailing out of port appeared to be moving on a curved surface. Also the shadow of earth on the moon during a lunar eclipse was curved and not straight.

This led to the problem of what kept people from falling off the spherical earth. One solution was to have earth at the center of the universe and have all objects naturally Afall@ towards the center of the universe.

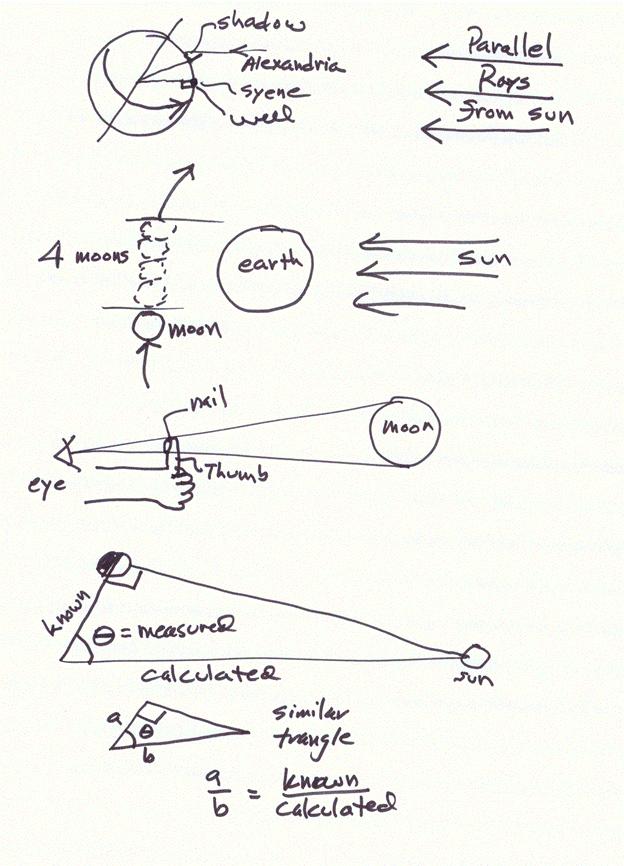
Eratosthenes, born in 276 BC, spent many years as the chief librarian in Alexandria. While in Alexandria, Eratosthenes heard about a well in the town of Syene in southern Egypt that had the remarkable property that sunlight would shine all the way to the bottom of the well one day a year B June 21. This never happened in Alexandria which was north of Syene.

Eratosthenes realized that the reason the sun could not be directly overhead Syene and Alexandria simultaneously because earth was curved. He used that information to measure angle the sun made with the Avertical@ at Alexandria on June 21, 7.2^o, and by knowing the distance between Syene and Alexandria was able to find the circumference of earth. The distance was in stades and the “exact” relationship between a stade and a mile is not known.

(7.2^o/360^o) = (Distance between Syene and Alexandria)/(earth=s circumference)

The actual value he got is somewhat clouded by the length of a Astade.@ But his value was reasonably close to 25,000 miles and his reasoning was impeccable!

Now it was known that during a lunar eclipse, the moon was fully in earth=s shadow for some time. By measuring the time it took for the moon to enter earth=s shadow and be completely in the shadow, about 50 minutes. And comparing that to the time the moon was completely in earth=s shadow, about 200 minutes, philosophers before the time of Eratosthenes had deduced that the earth was 4 times bigger than the moon.

Thus earth=s diameter 8000 miles and the moon=s diameter, 2000 miles, were known a couple of hundred years before the current period, BC.

Given that Eartosthenes now knew the diameter of the moon, he could easily deduce how far away the moon was from earth. The moon could be blocked out by a fingertip at an Arm=s length, a ratio of about (fingertip/arm=s length) = 1/100. This equals the ratio (moon=s diameter)/(distance to moon). Thus Eratosthenes found that the moon has about 100 times 2000 miles from earth, 200,000 miles.

Aristarchus had used the following geometrical argument to deduce the ratio of the distance of the moon from earth to the distance of sun from earth. He did this by noting that when half the moon was lit by light from the sun, the earth, moon, sun system formed a right triangle. He measured the angle between Earth and Sun and got 87^o (the actual angle is closer to 89.85^o) and deduced that the sun was 20 times further from earth than the moon. The actual value is about 400 times further or 80,000,000 miles.

Once the distance between earth and moon were known, it was easy to estimate the diameter of the sun since during a solar eclipse, the moon’s apparent size is just about the same as the apparent size of the sun, that is they subtend the same angle in the sky. Therefore the ratio of (moon’s diameter)/(sun’s diameter) = (distance between earth-moon)/(distance between earth-sun).

The motion of the planets

The Greeks and many other philosophical thinkers viewed the circle as perfect and since the heavens were the realm of perfection, decreed that orbits of heavenly bodies had to be circular with earth stationary at the center of the universe.

Question: Why did people care about accurate predictions for planetary motion?

The accurate prediction of the location of planets in the future and in the past based on their current locations were necessary for casting “accurate” horoscopes. People who rose to prominence, would often want to know the sign they were born under. Also, horoscopes were used to plan future significant events. The roots of astronomy are deeply entangled with the early fortune telling of astrologers!

Mars going around earth presented a problem for the ancients because at various times Mars moved backwards, retrograde motion, because it moved slower than earth and orbited, as we know outside of earth, as both went around sun.

Epicycles, circles on circles, were used to Afix@ the errors of the geocentric solar system.

Ptolemy in around 100 AD developed a set of tables that used dozens of circles on circles to construct a geocentric model that was the most accurate predictor of planetary motion available for the next 1500 years!

Note that circles were decreed because they were perfect and simple but the model became a parody of simplicity by having separate centers for different planets and all sorts of complicated constructs to fit the data!

Ptolemy and his tables were the last word in astronomy until Copernicus published his opus, De revolutionibus orbium coelestium (On the Revolutions of the Heavenly Spheres) in 1543. Copernicus was on his death bed when he finally got to see a printed copy of his book.

Copernicus argued that it would be simpler to have sun as the center with the planets orbiting sun. Though his model got rid of some of the epicycles, Copernicus still needed artifacts to get the predictions of his heliocentric solar system to be in reasonable agreement with observations because he still had the planets moving in circular orbits.

The next two major players in the development of our modern view of the solar system were Tycho Brache and Johannes Kepler. Tycho was the premier observational astronomer of his day and made the best naked eye measurements of planetary motion using instruments he designed and constructed by craftsmen who worked for him. His data was the best “naked eye” observations ever made. He collected data nightly for over 20 years and his observations were accurate to (1/30)^o, about 5 times better than any previous observations.

Kepler joined Tycho in 1600 just a few months before Tycho died of a burst bladder. Kepler, an adroit mathematician, thus suddenly found himself in possession of the best astronomical data ever assembled. As Kepler worked to find a model that could accurately fit the motion of the planets that had been so carefully chronicled by Tycho Brahe, he was stymied by consistent tiny errors in the orbit of Mars. Kepler, like all his predecessor’s, was operating under the premise that Mars moved in a circular orbit.

It is important to appreciate that for most purposes mars= orbit was very, very circular. The difference between the major and minor axis for mars is about 4%. Brahe=s measurements were accurate enough to make it impossible for Kepler to fit the motion of mars= orbit to a circle but instead forced him, after eight years of toiling, to the conclusion that mars orbits the sun in an elliptical orbit with the sun at a focus.

Kepler, in 1609, summarized his eight years of work into three succinct quantitative laws:

1. Planets sweep out equal areas in equal times. This means that planets move faster when they are closer to sun and slower when farther away. (Implied in this was some hint that sun=s effect was Abigger@ when the planet was closer.)

2. The period of orbit squared divided by the radius cubed was the same for all planets.

3. The planets orbited sun in ellipses with sun at a focus.

Isaac Newton in 1666 showed that all of Kepler=s laws could be derived by assuming that forces cause acceleration, F = ma, and that the gravitational force was given by,

F = GmM/d².

Newton showed that the same force that caused objects to fall on earth caused the planets to orbit sun. The heavens were not bound by different laws than those that operated on earth.

For the next 200+ years, scientists copied Newton and developed mathematical representations for all sorts of physical situations which culminated in 1864 when James Clerk Maxwell published the 4 equations which explain all electric and magnetic phenomena and predicted the existence of electromagnetic waves.

Light, what is it and how does it travel?

People speculated about the nature and speed of light for centuries. But the first evidence that light had a finite speed came from observing eclipses of one of Jupiter=s moons, Io. Ole Romer was confronted with data which suggested that Io passed behind Jupiter Alate@ when Jupiter was further from Earth. Using the data for these eclipses, Romer calculated a speed for light of 190,000 km/sec compared to its actual speed of 300,000 km/hr. In 1676 he correctly predicted that a certain eclipse of Io would be ten minutes Alate@ thus proving that light had a finite speed.

From the seventeenth to nineteenth centuries, more and more evidence piled up demonstrating the wave nature of light. Maxwell=s equations proved beyond any reasonable doubt that light was just a particular part of the electromagnetic spectrum.

Light travels unfathomable distances from stars to Earth. The obvious question was, Awhat was the medium through which light traveled?@ The idea that light could travel through a vacuum was anathema to scientists so they invented the Aluminiferous ether@ as the medium that permeated the universe and allowed light to travel through interstellar space.

By analogy with other mediums through which waves traveled, the ether had to be Astiff@ because light had a gigantic speed, while at the same time allowing Earth to move around the Sun with no apparent friction!

Michelson and then Michelson and Morley did very careful experiments to measure the speed of Earth through the ether between 1881nd 1887 they could not detect any difference in light transit times for the two perpendicular paths.

Swim 5 ft/sec, current is 3 ft/sec, swim 100 feet directly across the river and back, compare the time for that swim with the time to swim 100 ft down river and back. The difference in time is analogous to the difference that Michelson and Morley were attempting to measure between the perpendicular light paths.

As it became more and more evident that motion through the ether was undetectable, physicists like Lorentz tried to imagine interactions between the ether and material bodies that would produce the null result. This lead to the Ahypothesis@ that the ether effected objects in just the right way to make the ether undetectable! Is this a testable hypothesis (1895)

Einstein meanwhile was thinking about light from a completely different perspective. He was trying to imagine what would happen if you were looking in a mirror and traveling faster and faster. When you reached the speed of light, you would no longer be able to see your reflection! This seemed impossible to Einstein so he postulated that light traveled through the vacuum without any ether and that the speed of light was the same for all observers regardless of their state of motion!