Lecture 7: Momentum, Center of Mass, Conservation of Momentum, Impulse, and Collisions

Don't Panic

Sections

1. Momentum
2. Center of Mass
3. Conservation of Momentum
4. Impulse and Collisions
5. Kinds of Collisions
6. Elastic Collisions of 2 Particles in One Dimension
7. Inelastic Collisions of 2 Particles in One Dimension
8. Catalog of Images

---

Momenutm

---

Momentum (usually symbolized by p) is a vector (see images) defined as follows:

p = m v,

where

m is mass which is a scalar.

v is velocity is a vector.

Note fake links are used to display vector quantities. The link color makes the symbol stand out and underlines it which is something like undersquiggle symbol for vector.

The magnitude of a vector is the symbol without the fake link.

Momentum is also called linear momentum to distinguish it from angular momentum which is the topic of Lecture 9: Rotational Dynamics.

The (instantaneous) time rate of change of momemtum p is symbolized

             dp 
             --
             dt

Which is a calculus notation---but we are NOT doing calculus, merely using the symbol that is commonly used for the time rate of change of momentum p.

If mass m is constant,

             dp
             --  = ma
             dt

Newton's 2nd law ``F=ma'' in more general form than introduced in Lecture 4: Newtonian physics is

                 dp
            F =  --
                 dt

            where F is the total force acting on an object.

This expression allows for non-constant mass though we will seldom/never make use of that generalization in this course.

---

Center of Mass

---

The center of mass of an object of whatever kind is a usefully defined point in the vicinity of the object. For some purposes, the object acts as if it were a point-mass at the center of mass.

Consider a system of particles that make up an object.

Question: ``Let's play Jeopardy: Any set of objects or a single object that a physicist (or anyone else for that matter) chooses to regard as one thing for some purpose/purposes. The purposes usually are for calculation of properties including often future and/or past behavior."

What is a __________________, Alex?

1. system
2. universe
3. mass



Answer 1 is right.

The particles could be bound pieces in a rigid solid or fluid elements in a sample of fluid (e.g., a drop: see images) in complex relative motion.

Actually drop is a sort of quasi-semi-rigid object since the surface tension force gives it quasi-semi-rigid shape.

The small parts (fluid elements) of the drop can be regarded as the parcticles of the system.

The particles are classical or macroscopic, and so we can use Newtonian physics.

It doesn't really matter for what the particle size is for derivations, except that they are small compared to the object itself.

They have to be small enough that they can be accurately treated as point-masses.

This is guaranteed if one takes the particles small enough that the center of mass is independent of independent of the particle size.

We do NOT need quantum mechanics: the particles need never be that small for macroscopic objects.

But the particles could be very small.

Or somewhat larger like billard balls (see images).

Just as an illustration of a system of particles consider this classical-gas animation gif.

The gas is classical since the particles are acting like little billard balls (at least schematically).



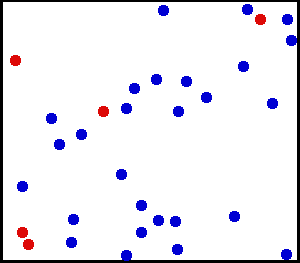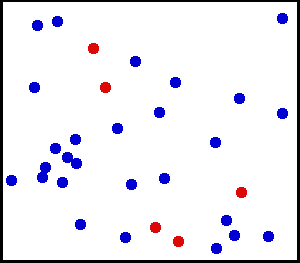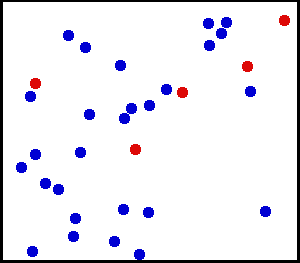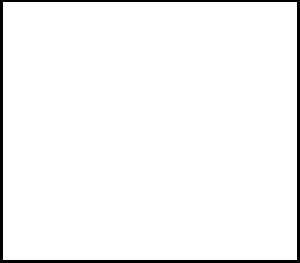
A schematic movie of a confined gas.

The molecules have kinetic energy which can be measured by temperature.

The microscopic collisions of the molecules give rise to macroscopic pressure which is a force per unit area on any planar slice through the gas.

Credit: Greg L. According to Wikipedia permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version.

Download site: Wikipedia: Image:Translational motion.gif.

Label each particle by i or some other general index j, k, l, m, n, etc.
Question: The expression

               sum_i x_i

    

means:
1. sum_i times x_i?
2. sum up all the quantities x_i.
3. take the product of all the quantities x_i.
4. All of the above.



Answer 2 is right.

Question: In the notation the instructor adopts for html

                y**n 

    

means
1. y times n.
2. y divided by n.
3. y to the power n.



Answer 3 is right.

I just find it easy to write and understand this notation in html

I prefer it to fussing with html superscripts: e.g., yⁿ.

In fact, using double asterisks for exponents is a usage in fortran which in its original version was the first higher-level programming language.

It is NOT a dead or obsolete programming language despite what C and Java programmers may think.

Fortran has merely become specialized as the programming language for numerical calculations.

It's actually a very simple programming language to learn.

For each particle i, we have Newton's 2nd law in its more general form:

            F_i =  (dp/dt)_i 

            where F_i is the total force acting on particle i

            and

            dp/dt_i is the rate of change of momentum of particle i.

Now F_i can be decomposed by

       F_i = F_i(ext) + F_i(int)  ,

       F_i(ext) is the sum of the external forces acting on particle i,

       F_i(int) is the sum of the internal forces acting on particle i.

       ``External'' and ``internal'' are relative to the system of particles.

Each F_i(int) is the sum of the forces exterted on particle i by all the other particles in the system.

       Thus,

       F_i(int) = sum_j F_ji

       where F_ji is the force of particle j on particle i.

       If we sum up F_i(int) for all particles, we get

       sum_i F_i(int) = sum_ij F_ji = 0 . 

Question: Why is

       sum_i F_i(int) = sum_ij F_ji = 0  ?

1. The instructor hasn't explained it yet.
2. We havn't thought of it yet.
3. The inter-particle forces cancel pairwise.
4. All of the above.



Answer 3 is right.

Answers 1 and 2 are answers of another question: ``Why don't we know why ... ?

By Newton's 3rd law for every force there is an equal and opposite force.

This is why the last sum equals zero.

For every F_kl in the sum, there is a F_lk=-F_kl and the two cancel out pairwise.

So if we sum

            F_i =  (dp/dt)_i

over all particles we get

       F(ext)= sum_i F_i = sum_i (dp/dt)_i = (dp/dt)

       where 

       F(ext) is the total external force,

       and dp/dt the total rate of change of momentum.

Two important results follow from this last equation.

First, say all the particle masses m_i are constants.

Then

       F(ext)= sum_i m_iF_i = m a_(cm)}

       where a_i are the individual particle 
       accelerations,

       m = sum m_i is the total mass of the system of particles,

       and a_cm is the 
       acceleration,
       of the
       center of mass

       defined by

       a_(cm) = ( sum_i m_i a_i)/m

In principle, the solution of

       F(ext)= m a_(cm)

gives

       r_cm = (sum_i m_i*r_i)/m

       center of mass itself

       (which is a mass-weighted average position for the particles) 

       and

       v_cm = ( sum_i m_i*v_i )/m
 
       the velocity
       of the 
       center of mass.

But note the solution of

       F(ext)= m a_(cm)

does NOT tell us what the individual particles are doing.

In most of our calculations in this class, we have assumed the objects act as point-masses.

We now see that most of our calculations apply to the centers of mass of the objects.

For example, when air resistance was neglected we found that thrown objects follow parabolic trajectories.

But that was treated them as point-masses.

Now we know that it is the centers of mass of those objects that were following a parabolic trajectories.

The overall motion may be complicated.

The object may be spinning or tumbling.

See for example, jugglers passing clubs at Wikipedia: Passing (juggling).

If non-rigid, it might be flexing in odd ways.
For example, high jumpers (see images) have to twist their bodies around to make sure that legs, arms, etc., don't hit the bar even though their centers of mass are going over.

Now I know what you are thinking---where are centers of mass?

For objects of high symmetry (e.g., uniform density cubes, spheres, disks, cylinders, hoops, etc.) the center of mass is at the obvious geometric center.

See list of moments of inertia (for high-symmetry objects)).

Question: A center of mass must be physically inside a the body it is a center of mass of.
1. Yes.
2. No.
3. Maybe.



Answer 2 is right.

Think of a spinning thrown hoop: e.g., a hula hoop.

For high symmetry objects consider the general formula for center of mass,

       r_(cm) = (sum_i m_i * r_i)/m

       with the origin at the geometric center and the
       object decomposed symmetrically.

       For every term m_k*r_k, there is a term  

       m_l*r_l = -  m_k*r_k ,

       and so all terms cancel out pairwise

       and r_cm = 0 which is the origin of the calculation.

For 1-dimensional objects, the calculation of center of mass is simpler:

                 sum_i m_i x_i
       x_(cm)} = ---------------  ,
                      m

       where the expression is no longer a vector equation.

For example, consider two point-masses along a massless bar:

       one is at 2.0 m from the left end  

         and has 5.0 kg mass;
       
       the other is at 6.0 m from the left end 

         and has mass 12.0 kg.

  The
  center of mass
  is 
             sum_i m_i x_i        m_1 x_1  +  m_2 x_2        5*2+12*6
  x_(cm)} = ---------------  =  ----------------------  =  ---------- = 82/17 = approx 5 m 
                  m                   m_1 + m_2                 17


        from the left end.

        Note the 
        center of mass
        is closer to the heavier point-mass as it should be for
        a mass-weighted average position.

For complicated objects, the center of mass can be difficult to calculate.

   There is a simple empirical procedure fer finding it for rigid bodies.

   Hang the body from a free pivot and let it come to rest.

   The center of mass will be
   directly below the pivot point.

   Now hang the body from another free pivot and let it come to rest.

   The center of mass will be
   directly below the pivot point again.

   From the intersection of the lines from the two pivot points to the ground, the
   center of mass
   can be located.

   Proof of this result seems to require considering 
   angular momentum
   and
   torque.

   These are subjects of
   Lecture 9:  Rotational Dynamics.

The second important result from equation

       F(ext)= sum_i F_i = sum_i (dp/dt)_i  = (dp/dt)

is the conservation of momentum in the absence of a net external force.

---

Conservation of Momentum

---

When

       F(ext) = 0 ,

       the equation

       F(ext)= sum_i F_i = sum_i (dp/dt)_i  = (dp/dt) 

       reduces to 

       (dp/dt) = 0 ,

       which implies that

       p = sum_i p_i = sum_i m_i v_i  = constant  ,


      or in other words, in the absence of a net external force

      total
      momentum 
      is conserved
      for the system. 

The conservation of momentum (in the absence of a net external force) is very useful in many contexts including simple calculations.

For example, consider two skaters initially at rest who push of from each other and go into motion (see image Wikipedia: Image:Skaters showing newtons third law.png and ice skating).

We assume frictionless ice and no air resistance.

No external forces can act on the two skaters.

The equation of conservation of momentum in this case simplifies to the 1-dimensional form

    m_1 v_1 +  m_2 v_2  =   m_1 v_1' +  m_2 v_2'

   where the left-hand side is pre-push-off and the right-hand side is
   post-push-off.

   In this case,

        v_1=v_2=0,

        v_1'=2.5 m/s,

        m_1=54 kg, 

        m_2=88 kg .

   We have one equation and one unknown (v_2'), we can solve for the 
   unknown.

   First

   0 =  m_1 v_1' +  m_2 v_2'  . 

   Thus, 

             m_1 v_1'          54*2.5
   v_2' = - -----------  = - ------------  = approx. - 1.5 m/s  .
               m_2               88

The two skaters pushing off from each other is actually an example of an inelastic collision in which kinetic energy

KE = (1/2)*m*v**2

increases---a case of inelastic collisions which is often omitted when inelastic collisions are considered in introductory physics courses.

Which it shouldn't be: think explosions (see images).

---

Impulse and Collisions

---

The impulse of a force is on a body is DEFINED by:

     J = integral of F over (Delta t) = F_(average) * (Delta t)

     where F_Average is the average force 

     and (Delta t) is the time over which it acts.

Remember in physics (see images), we just define quantities when we need them.

From calculus---of which we will do NONE---it follows from Newton's 2nd law when F is the total force that

     J = F_Average * (Delta t) = Delta p

     where Delta p is the change in momentum of the object in time (Delta t).

The last result can be derived from calculus which is beyond our scope, but we can give an approximate derivation that is reasonably cogent.

         Just as we obtained instantaneous velocity and acceleration
         from a limit, we obtain 

         dp/dt  = limit (Delta t goes to 0) Delta p/(Delta t)

         Now 
   
         (dp/dt)_Average  =  Delta p/(Delta t) .

         The non-rigorous bit is that we havn't specified 
         how to take the average in order to make this last
         equation exact.

         But it can be done.


         Now

            F_Average =  (dp/dt)_Average

            and so

            F_Average =  Delta p/(Delta t) 

            and


            J = F_Average * (Delta t) = Delta p .

The concept of impulse is most useful when you have a very strong force that acts for a relatively short time and dominates the behavior.

In such cases, the strong force F_Average(strong)>>F_Average(other).

     Thus

      J = Delta p = approximately F_Average(strong) * Delta t

     over the time Delta t. 

Consider a baseball ball: see image.

As it travels from pitcher to the bat to the , the forces of gravity and air resistance are always acting.

They do NOT turn off during the ball-bat interaction (i.e., the collision), but during that short time of interaction, they are negligible for the ball behavior.

    Example:  There is a ball of hit by a bat:

    ball mass = 0.14 kg ,

    Delta t = 1.6*10**(-3) s 

     v_initial = -38 m/s (or about 86 mi/h)

     v_final = 58 m/s

        (all as measured by 

         high speed photography (see image)

         or high-speed filming.)

      We can calculate the bat-ball collision force

         with the ASSUMPTION that the other forces are negligible 

         during Delta t.


      F = J/(Delta t) = (m*v_final - m*v_initial)/(Delta t)

        = 0.14*[58-(-38)]/[1.6*10**(-3)]

        = approximately 10**4 N
 
        = 8400 N more exactly


       What's the gravity force?

       F_g = mg = approximately 1.4 N

       Air resistance is comparable for smaller than gravity.

       During the 1.6*10**(-3) s interaction, gravity and air resistance
       were negligible and can be neglected.

   

In physics, a collision is an interaction during which the collision forces dominate the behavior during the collision.

In an ideal collision only the collision forces are significant.

The COLLISION APPROXIMATION is to only consider the collision forces.

If you regard the colliders are collectively being one system, then in the COLLISION APPROXIMATION all the forces are internal to the system and there is conservation of momentum.

Using conservation of momentum often helps in solving collision problems.

---

Kinds of Collisions

---

In the COLLISION APPROXIMATION (meaning we assume conservation of momentum for the system of colliders), there are several types of collision

1. Elastic Collision: In this kind of collision, kinetic energy is conserved.

   The classical gas gif animation schematically shows this behavior.

   

   A schematic movie of a confined gas.

   The molecules have kinetic energy which can be measured by temperature.

   The microscopic collisions of the molecules give rise to macroscopic pressure which is a force per unit area on any planar slice through the gas.

   Credit: Greg L. According to Wikipedia permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version.

   Download site: Wikipedia: Image:Translational motion.gif.

2. Inelastic Collision: In this kind of collision, kinetic energy is NOT conserved.

   See images at Inelastic Collision.

   Often kinetic energy is lost as heat.

   It can also be lost in changing the structure of the colliders.

   It can also go into the rotational kinetic energy and vibrational kinetic energy of the colliders.

   But kinetic energy can also increase as in explosions (see images) or from a spring like action as in our skater example.

3. Completely Inelastic Collision (see images): In this kind of inelastic collision, kinetic energy is NOT conserved and the colliders stick together.

   The translational kinetic energy is always reduced in a completely inelastic collision.

   There is a proof of this, but it involves some subtleties, and so the following is optional.

   First, translational kinetic energy is the just the kinetic energy of the center of mass.

   rotational kinetic energy and vibrational kinetic energy are excluded.

   Now the total momentum is conserved through the collision process that leads all the particles sticking together because no external forces act.

   This momemtum is

   
                   p = sum_i m_i*v_i  = m*v_cm  
   
                   where m is total mass and v_cm is the velocity
                   of the center of mass. 
   
              

   The total translational kinetic energy before the collision process begins is:

   
                  KE_{before} = sum_i (1/2)*m_i*v_i**2
   
                              = sum_i (1/2)*m_i*
   
                                 [ (v_cm+delta v_i) DOT (v_cm+delta v_i) ] ,
   
                  where delta v_i is the vector difference of 
   
                  v_i from v_cm
   
                  and
   
                  here ``DOT'' indicates
   
                  dot product.
   
                  Note (a DOT b)=ab*cos(theta) where theta is the angle between
   
                  a and b and a and b are, respectively, 
                  the magnitudes of a and b.
   
                  Note also that v_i**2 = v_i DOT v_i since the angle between
                    a vector and itself is zero, and so the cosine is 1 in the
                   dot product.
   
                  Now with that machinery, we find
   
                  KE_{before} = sum_i (1/2)*m_i*v_i**2
       
                              =     sum_i (1/2)*m_i*v_cm**2
   
                                  + (sum_i m_i delta v_i ) DOT v_cm
   
                                  + sum_i (1/2) (delta v_i)**2   .
   
                  Now sum_i (1/2)*m_i*v_cm**2 = (1/2)m*v_cm**2 is the translational KE of the
                  center of mass.
   
                  Since the velocity of the
                  center of mass
                  is conserved, (1/2)m*v_cm**2 is conserved.
   
                  Since all the particles are stuck together after the 
                  collisional process, the post-process total 
                  translational kinetic energy
                  is just (1/2)m*v_cm**2:
   
                      KE_{after} = (1/2)m*v_cm**2 .
                 
                  Now 
   
                      sum_i m_i delta v_i 
   
                    = sum_i m_i ( v_i - v_cm )
   
                    = (sum_i m_i  v_i) - (sum_i m_i v_cm)
   
                    = mv_cm - v_cm
   
                    = 0
   
                  So finally
   
                  KE_{before} = KE_{after} + sum_i (1/2) (delta v_i)**2   .
   
                  The last term is always positve or zero, and so
   
                  KE_{before} > =  KE_{after} .
   
            
   
       

In dealing with collisions, conservation of momentum gives you as useful constraint.

But you cannot predict the outcome of a collision, just using conservation of momentum.

Some other information is required.

Either about the collision interaction itself or about the post-collision results.

We will now consider some collision examples, but only for collisions in 1 dimension.

---

Elastic Collisions of 2 Particles in One Dimension

---

The case of the elastic collisions of 2 particles in one dimension is special in that the 2 conservation equations (those momentum and kinetic energy) dictate the post-collision conditions given the pre-collision conditions.

In all other cases that the author knows of, some post-collision information is needed to solve for the post-collion conditions or was has to treat the collision event itself in detail: i.e., treat the forces and accelerations through the collision.

For our case, the two conservation equations for particles 1 and 2 are

       m_1*v_1 + m_2*v_2 =  m_1*v_1' + m_2*v_2'        (6.1)

         for momentum 

         and

      (1/2)*m_1*v_1**2 + (1/2)*m_2*v_2**2 =  (1/2)*m_1*v_1'**2 + (1/2)*m_2*v_2'**2  (6.2)

         for kinetic energy,
 
         where the primes indicate post-collision and the unprimes pre-collision. 

      Here we assume we know the masses and know the past:  thus 

      v_1' and v_2' are the unknowns.

We have two unknowns in two equations and can solve for the unknowns.

The complication is that one equation is not linear.

We need a trick for a quick solution.

Rearranging the equations and simplifying gives

       m_1*(v_1 - v_1') = m_2*(v_2 - v_2')        (6.3)

         and

       m_1*(v_1**2 - v_1'**2) = m_2*(v_2**2 - v_2'**2)        (6.4)

Now we make use of the difference of squares formula (which is our trick)

     (a+b)*(a-b)=a**2-ab+ba-b**2=a**2-b**2  ,

       we divide equation (6.4) by equation (6.3) to get

     v_1 + v_1' = v_2 + v_2'       (6.5)

       of
  
     v_2' - v_1' = -(v_2 - v_1)      (6.6) 

Dividing equation

---

Inelastic Collisions of 2 Particles in One Dimension

---

---

Catalog of Images

---

1. ballistic pendulum No images.

2. billard balls Images.

3. gravity assist Images.

4. gymnastics The image of the boy on the pommel horse illustrates the use of center of mass. If he's a rest as he seems to be, his center of mass must be above his hand for he'll torque over.

5. high jump High jumper images illustrating center of mass going over the bar.

6. high speed photography Great Muybridge film.

7. inelastic collision Images and an animation.

8. skater image Illustrates Newton's 3rd law.

9. Temperature Gas gif animation.