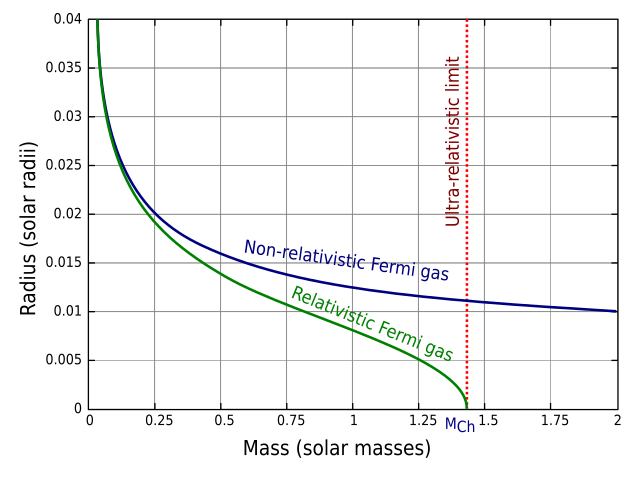
Caption: The mass-radius relationship a fiducial white dwarf modeled with an absolute zero (i.e., T=0 K) Fermi gas pressure.

Features:

1. White dwarfs are held up in hydrostatic equilibrium against gravitational collapse under their own self-gravity by a quantum mechanical pressure of degenerate electrons that is only slightly temperature dependent: the degenerate electron gas pressure.

   A gas with such a pressure is called a Fermi gas.

   Fermi gas pressure is very unlike ideal gas pressure and radiation pressure most obviously because those pressures depend strongly on temperature.

2. The Fermi gas pressure of white dwarfs causes them to decrease in radius as their mass increases. The upshot is the mass-radius relationship illustrated in the plot.

   The relationship is shown for the limit of absolute zero (i.e., T=0 K).

   However, for the Fermi gas in white dwarfs even temperatures of ∼ 10**5 K are close enough to absolute zero (i.e., T=0 K) that the shown curves are appoximately valid for said white dwarfs.

3. The green curve is the relativistic case and closely approximates real white dwarf behavior.

4. The blue curve is the non-relativistic case which is NOT realistic when it diverges from the green curve.

5. The calculations were done with 2 as the mean molecular weight per electron.

   This is the fiducial value for matter that is NOT hydrogen.

   White dwarfs are usually carbon-oxygen white dwarfs (made up mostly of carbon and oxygen) and oxygen-neon-magnesium white dwarfs (made up mostly of oxygen, neon, and magnesium). All the elements making up these kinds of white dwarfs have mean molecular weight per electron of ∼ 2. Thus, 2 is the appropriate fiducial mean molecular weight per electron for white dwarfs.

   But note that most white dwarfs have an outer shell of hydrogen or helium, and so those elements are what one detects in most white dwarf spectra.

6. The distribution of masses of white dwarfs strongly peaks at ∼ 0.6 M_☉ (see Wikipedia: White dwarf: Composition and structure).

7. Note that 0.01 solar radii ≅ 1 Earth radius---more exactly the solar radius R_☉ = 6.957*10**5 km = 109 R_eq_⊕ (see also Wikipedia: Sun).

   Thus, white dwarfs are typically Earth size even though they have masses of like those of a star.

8. Given the last remark, white dwarfs have must have super high density.

   Typically their densities are in the range 10**4--10**8 g/cm**3 (see Wikipedia: White dwarf: Composition and structure).

   These densities are very high compared to terrestrial densities for solids which are typically between 1 and 20 g/cm**3---the densest element at standard ambient temperarue and pressure (SATP, T=298.15 K=25 C, P=100 kPa=14.504 psi) is osmium (Os) with density 22.59 g/cm**3.

   The white dwarf densities are also high compared to central densities of stars---for example the central density of the Sun is about 160 g/cm**3 (see Wikipedia: Sun).

   White dwarfs are the least extreme kind of compact remnant of stars. The more extreme kinds are neutron stars and black holes which have even higher densities.

9. The relativistic case for white dwarf radius shows that there is an upper mass limit for white dwarfs of about ∼ 1.4 solar masses. (i.e., ∼ 1.4 M_☉).

   This limit is called Chandrasekhar mass.

   The exact value of the Chandrasekhar mass depends on how many corrections for small effects are included in the calculation and the mean molecular weight of the white dwarf being modeled.

   The value given by the plot is ∼ 1.44 M_☉.

   The fiducial value is 1.4 M_☉.

10. What happens if a white dwarf mass increases toward the Chandrasekhar mass?

    Well for the absolute zero (i.e., T=0 K) Fermi gas model, the white dwarf radius will shrink and reach exactly zero at the Chandrasekhar mass.

    But the absolute zero (i.e., T=0 K) Fermi gas model only approximates reality.

    Actually, when the mass gets nearly to the Chandrasekhar mass, a white dwarf will, depending on various factors, collapse to form a neutron star or explode as a SNe Ia (Type Ia supernova) due to runaway picnonuclear burning (i.e., low-temperature nuclear burning).

    White dwarfs with masses greater than the Chandrasekhar mass may exist though they are probably rather rare. Fast rotation or some other process may allow white dwarfs to exceed the Chandrasekhar mass which was derived for a non-rotating, simple white dwarf model.