Logarithms

John Napier (1550--1617) Credit: ?; download site St. Andrews Napier biograph

          Logarithms were invented by John Napier (1550--1617) and first published in Mirifici logarithmorum canonis descriptio in 1614. They were intended to be an aid to practical calculations. The word logarithm derived is from the Greek combination of two Greek words: logos meaning in this context proportion (and not ``the Word'' as the New Testament translates it); and arithmos meaning arithmetic (Ba-717). Kepler used logarithms in calculating the Rudolfine Tables (1627) ( Ca-308). Napier and Kepler's logarithms were, alas, very different in appearance from the modern versions.

          A LOGARITHM of number is the EXPONENET of a fixed BASE to which that base must be raised in order to produce that number. An example clarifies. Say we have a number x, then its logarithm y in base 10 satisfies

      x=10y .

The inversion of the above formula is written

      y=log(x) , 

where ``log'' is the logarithm function that we invent to allow us to right this formula. The log function is TRANSCENDENTAL like sine and cosine: i.e., you can't calculate log(x) by a finite number of algebraic operations in general. The logarithms of numbers must in general be calculated approximately by numerical methods.

          But some logarithms are easy. The base 10 logarithms of

   1, 10, 100, 1000, 1/10, 1/100, 1/1000 are, respectively, 
 
   0,  1,   2,    3,   -1,   - 2,     -3  .

Non-integer logarithms are not so easy to calculate---but your calculator will do it for you or you could look them up in a table.

          There are only two common bases in use: BASE 10 and BASE e (the base of natural logarithms). Base e is extremely important in many fields: physics, biology, banking. But we'll leave base e for another day. The astronomical magnitude system uses approximately BASE 2.512.

          Logarithms were first introduced to ease calculations. They turn multiplication and division into addition and subtraction. For example, consider two numbers x_1 and x_2 and their respective logarithms y_1 and y_2:

x_1*x_2=(10**y_1)*(10**y_2)=10**(y_1+y_2)   ;

x_1/x_2=(10**y_1)/(10**y_2)=10**(y_1-y_2)   . 

One finds out the product and quotient by looking up the antilogarithms of y_1+y_2 and y_1-y_2 in a table.

          For simple calculations logarithms are seldom used nowadays. But yours truly remembers when log tables were still handed out so that students could use them when writing tests: circa 1972. In computer calculations logarithms are still often used however.

          But there are two other important uses of logarithms:

(1) the logarithm function turns up as a physical function in many contexts (i.e., some physical quantities vary as the logarithm of other quantities);

(2) logarithmic representation on graphs.

Use (1) is in fact the fundamentally most important use of logarithms of all. But we'll leave it to another day.

          Logarithmic graphing or log plots are a powerful representational tool when dealing with quantities that vary by many orders of magnitude (i.e., powers of 10) and you want to see clearly on the same plot how they vary on all scales. To achieve this effect, you plot the logarithm of the quantity rather than the quantity directly. Usually base 10 is used. Base e is used sometimes if the quantity varies exponentially. Base 2.512 is used in astronomy for magnitudes. For a base 10, an increase of 1 on the plot is an increase by a factor of 10; an increase of 2 on the plot is an increase by a factor of 100; etc. A unit on a base 10 log plot is often referred to as a dex: one talks of 1 dex (factor of 10), 0.5 dex (factor of 3), 3 dex (factor of 1000), etc.

          In astrophysics, where quantities often vary astronomically, log plots are common. As an example look at a logarithmic plot of the mean solar system relative abundances of the elements by number at the site of Andrew Cowley, University of Michigan. The relative abundances have an important STORIES to tell that we will return to throughout our course.

          The abundances were determined by studies of the Sun and carbonaceous chondrite meteorites. Such meteorites it is though were never heated above about 500 K (Se-556). Thus, except for volatiles (H, He, and other noble gases) probably closely resemble the primordial solar composition which may have be fairly uniform.

          For the plot the relative scale hydrogen (H) is set arbitrarily by astronomical convention to 10**12 with logarithm 12. You should be able to see that helium (He) is only 1/10th of the abundance of hydrogen (H). Oxygen (O) is about 3 dex down from H: there is only about 1 oxygen atom for every 1000 hydrogen atoms in the solar system. Among the heavier elements iron (Fe) is most abundant: but it's 4.5 dex down from H.

          You can see that the solar system is overwhelmingly hydrogen and helium. But, of course, the elements arn't homogeneously distributed. The Sun and the gas giant planets (Jupiter, Saturn, Uranus, and Neptune) have compositions that are close to the mean solar system abundances. The rocky bodies (Mercury, Venus, Earth, Mars, moons, and asteroids) have lost most of their hydrogen and helium. Those elements mainly escaped the hot, early Earth: the heat caused the light atoms that were NOT bound tightly in compounds to achieve escape velocity. Most of the hydrogen we have left is locked into water (H_2O) and other compounds. The elements that are non-volatile (i.e., don't evaporate easily) in pure form (e.g., metals) or in readily formed compounds (e.g.,, oxygen in silicates, the commonest form of minerals in rock) probably have relatively close to their the mean solar ratios on Earth. That implies that there should be a lot of iron on Earth: more than we ever notice on the surface. Where is it?

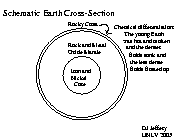
          Mostly in the deep interior (i.e., the CORE) we believe---we have never drilled so deep, of course, and are relying on indirect evidence. The early hot Earth was subject to chemical differentiation. The denser material iron sank while the lighter material---mainly silicates (compounds of silicon (Si) and oxygen (O))---floated up to form the surface layer. (Remember oil floats on water.) The chemical differentiation was not perfect, of course.