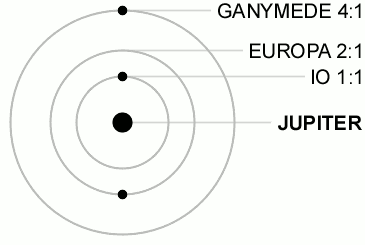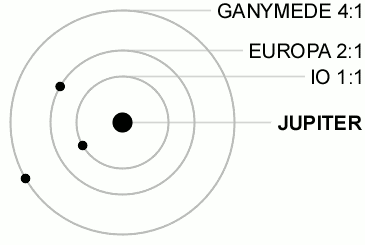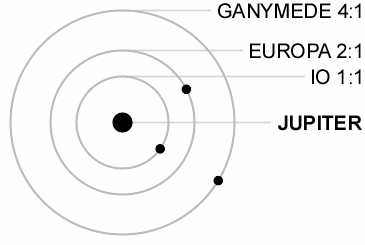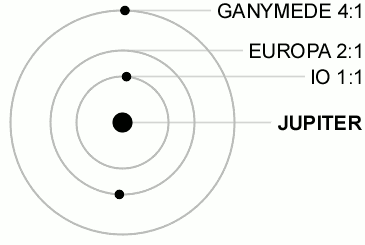
Caption: An animation illustrating the 1:2:4 Laplace resonance of the orbits of Jupiter's Galilean moons Io, Europa, and Ganymede.

The 1:2:4 Laplace resonance (which is special set of gravitational perturbations) forces the orbital periods of these Galilean moons to be in the ratio 1:2:4 for, respectively, the orbital periods of Io (orbital period 1.769 days), Europa (orbital period 3.551 days), and Ganymede (orbital period 7.155 days).

Gravitational perturbations (and maybe other perturbations) constantly perturb the actual ratio away from the exact 1:2:4 ratio, but the 1:2:4 Laplace resonance is stable meaning that a restoring force (which is the special set of gravitational perturbations of the 1:2:4 Laplace resonance) constantly drive the system back toward the exact 1:2:4 ratio.

The actual precisely measured ratio at present is 1:2.007:4.045. So not exactly the 1:2:4 ratio as expected, but very close to that ratio.

The outermost Galilean moon Callisto (orbital period 16.69 days which is 9.435 in units of Io's orbital period) has avoided being in a Laplace resonance with the 3 inner Galilean moons.

Probably in Callisto's case, gravitational perturbations overcome any Laplace resonance effect.

The animation gives the exact 1:2:4 Laplace resonance for illustrative reasons.

You can see the 1:2:4 ratio if you concentrate on two of the Galilean moons at once.

All the Galilean moons are tidally locked to Jupiter.

Thus, their axial rotational periods are the same length as their orbital periods and they always turn nearly the same side to Jupiter.

Credit/Permission: User:Matma Rex, 2011 / Public domain.
Image link: Wikipedia.
File: Jupiter images file: jupiter_galilean_moons_resonance.html.