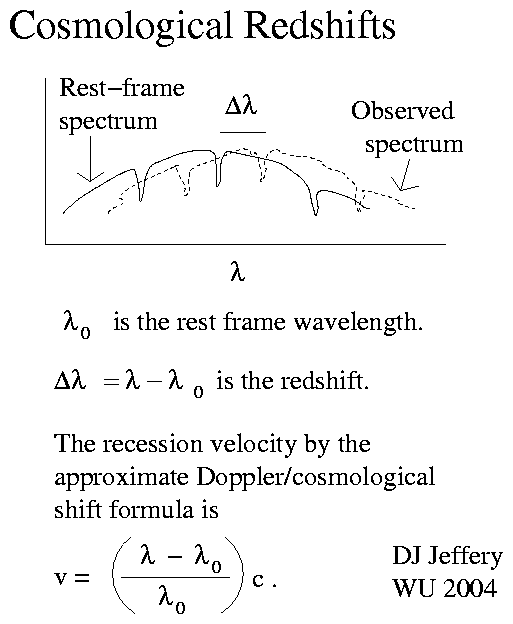
Caption: The cosmological redshift z illustrated using a schematic absorption line spectrum.

Features:

1. The cosmological redshift is the increase in wavelength of electromagnetic radiation as it propagates through expanding universe

   Space literally grows under the electromagnetic radiation stretching out the waves.

2. The cosmological redshift is NOT the Doppler effect.

   The causes of the two effects are different: the cosmological redshift is caused by the growth of space which is NOT an ordinary velocity and the Doppler effect is caused by an ordinary relative velocity between source and observer.

   The growth in space between source and observer is called a recession velocity. To repeat, it is NOT an ordinary velocity and it can exceed the vacuum light speed (which is not a violation of special relativity because it is NOT an ordinary velocity).

   Note also that the cosmological redshift and Doppler effect have have different formulae relating recession velocity/relative velocity and wavelength shift.

3. However, the cosmological redshift and the Doppler effect are often confused with some people calling the cosmological redshift a Doppler effect.

   Why is this?

   The main reason is that the two effects have the same formula relating recession velocity/relative velocity to redshift parameter z (which we specify below) to 1st order in small redshift parameter z.

   To explain 1st order agreement in this context, we note that both formulae can be written in the power series expansion form f(z) = f_1*z + f_2*z**2 + f_3*z**3 + ... as long as z ≤ ∼ 1.

   The exponent z is raised to defines the order of the term. The coefficients of the terms are subscripted by the order of the term.

   To agree to 1st order means that the f_1 coefficient is the same in both formulae, but the higher order coefficients do not agree.

   As z → 0, the difference between the two formulae eventually starts decreasing like z**2 and the relative difference like z because the terms of order ≥ 3 become smaller at a faster rate than lower order terms.

   The agreement of the two formulae to 1st-order allowed early investigators of the universal expansion to interpret their data semi-correctly without being clear about the nature of the universal expansion as a growth of space.

   The conceptual confusion between the cosmological redshift and the Doppler effect was cleared up pretty soon---except for those folks who keep calling the former the latter out of laziness.

4. However, there is an observational confusion between the two effects.

   Virtually all astronomical objects have peculiar velocities relative to their local inertial frames. So there is virtually always a Doppler shift of wavelength.

   For astronomical objects in the Local Group of galaxies there is almost no cosmological redshift because the Local Group is a gravitationally bound system.

   Only for farther away astronomical objects does the cosmological redshift turn on. But then you have both effects and the two have to be deconvolved.

   For cosmologically nearby objects, the deconvolution can be difficult because the two effects are often of nearly the same size.

   However, for farther objects, the cosmological redshift dominates and the effect of the Doppler effect can usually be neglected.

   For objects at ∼ 100 Mpc, the Doppler shift is about 10 % of the cosmological redshift (see Wikipedia: Hubble_constant.JPG). As one increases distance above 100 Mpc, the percentage Doppler shift decreases with distance and soon becomes negligible.

5. The redshift parameter z is defined by the formula

   z=(λ_observed-λ_rest)/λ_rest  ,
   

   where λ_observed is observed wavelength and λ_rest is the wavelength in the rest frame of emission.

6. The λ_rest values of the atomic lines that cause the absorption lines (i.e., the deep narrow troughs) in absorption line spectra are known to high accuracy from laboratory measurements.

   Using these λ_rest values, z can be determined to high accuracy in many cases even for cosmologically remote objects.

   Consequently, redshift parameter z is considered a direct observable.

7. Hereafter, we will just use z the cosmological redshift unless otherise indicated. This is a common usage when the meaning is clear.

8. The redshift velocity is defined by the formula

   v_red=zc  , where
   

   c is vacuum light speed.

   The recession velocity v_rec = v_red to 1st order in small z.

   When z is due to the Doppler effect ordinary relative velocity equals v_red to 1st order in small z too.

   Thus, we see the 1st-order agreement of the formulae for cosmological redshift and Doppler effect mentioned above.

9. For z = 0.5, the redshift velocity is about 10 % larger than the recession velocity. As z → 0, the difference goes to zero linearly with z as it should for 1st-order behavior.

   For z > 0.5, the difference increases between the two types of velocity increases rapidly.

   We only know these quantitative results from the concordance model (AKA Lambda-CDM model) (of cosmology) since recession velocity is NOT a direct observable in general---it is a model-dependent quantity.

10. In fact, cosmological redshift z is overwhelmingly the most easily obtained cosmological distance measure.

    All other cosmological distance measures are either model-dependent or very hard to obtain. These cosmological distance measures include the model-dependent proper distance (just the ordinary distance measured at one instant in time).

    Because proper distance is model-dependent it is conventional among astronomers to specify the "distance" to an astronomical object in the cosmological realm by just specifying z.

    The other cosmological distance measures (including proper distance) can be calculated using z and a cosmological model.

    At present, the overwhelmingly favored cosmological model is the concordance model.

11. We should note that z = 0 is the very nearby observable universe: essentially just the Local Group.

    The is no single definition of the local universe, but one useful definition is the region of observable universe at z ≤ 0.5 (see /astro/cosmol/local universe).

    Beyond the local universe is the cosmologically remote observable universe.

    The edge of the observable universe is at z = ∞ by conventional definition.

    In fact, the observable universe probably doesn't go quite that far for reasons we will discuss below.

12. Recall that looking out into observable universe is also looking back in time since vacuum light speed is finite. It takes a finite time for the electromagnetic radiation that gives rise to z to reach us from its source.

    Thus z is also a measure of the travel time which is called the lookback time. Lookback time is, in fact, one of the cosmological distance measures for cosmological remote objects.

    The current cosmic time minus the lookback time is the the cosmic time or epoch is when the source emitted the electromagnetic radiation we receive.

    Neither the lookback time nor the epoch of emission are direct observables for cosmologically remote regions.

    They can be calculated from using z and a cosmological model.

    To repeat, at present, the overwhelmingly favored cosmological model is the concordance model.

    Among astronomers, it conventional to specify the epoch of emission from a cosmologically remote astronomical object just by specifying z.

13. In expanding universe cosmology, there is an important general relation between cosmological redshift z and the cosmic scale factor a(t):

                 1 + z = a(t=present)/a(t)  ,
             

    where a(t=present) = 1 is the current cosmic scale factor (set to 1 by convention) and a(t) is the cosmic scale factor at the cosmic time t when the electromagnetic radiation that gave rise to the measurement of z started out.

14. The general relation is easily proven.

    Given that the wavelength of electromagnetic radiation expands with the space it travels through, then

              a(t=present)/a(t) = λ_observed/λ_rest  = λ_observed/λ_rest - 1 + 1
    
                                = (λ_observed-λ_rest)/λ_rest + 1
    
                                = z + 1 QED.
              

15. We can now see why z = ∞ is probably not realistic.

    It implies a(t=0) = 0 which means the observable universe started from a region of zero size (i.e., a point) and therefore infinite density.

    We believe that general relativity (or variant thereof) on which cosmological models are based must fail before infinite density is reached.

    Therefore we cannot run the clock on these models back to time zero and therefore they do not extend out to z = ∞.

    We can run the models back to a tiny fraction of a second (see Wikipedia: Graphical timeline of the Big Bang).

16. The farthest z which we can actually measure to at present is z ≅ 1100 which is when recombination occurred (Wikipedia: Recombination).

    The edge of the observable universe is defined by limit of how far we could see if the pre-recombination epoch were transparent to electromagnetic radiation.

    But it wasn't transparent until the recombination epoch.