Precession of the Equinoxes

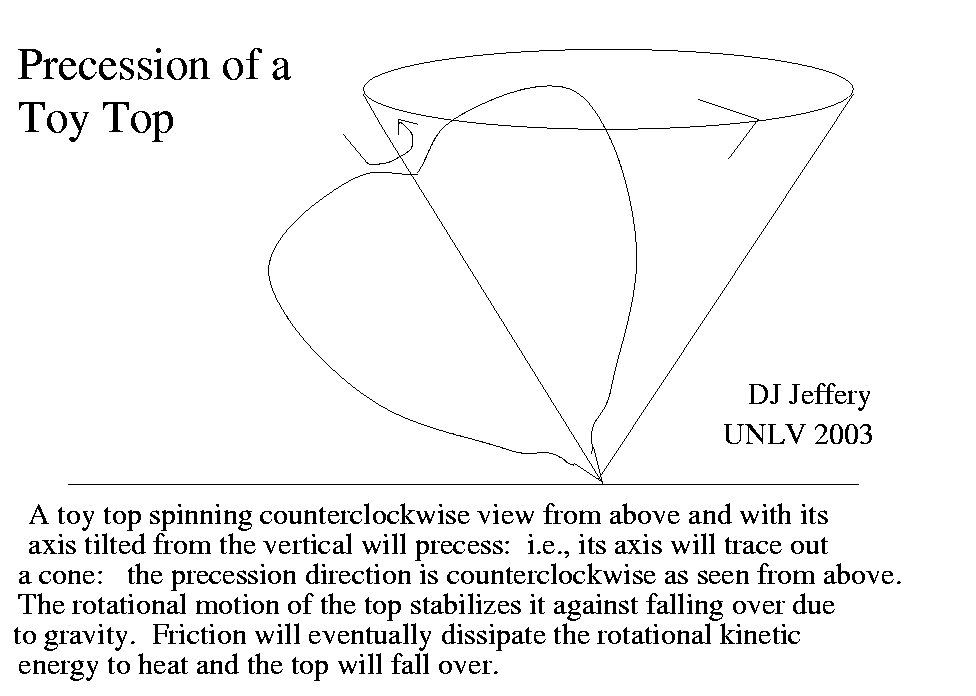
The Precession of the Equinoxes is the traditional name for precession of the Earth's axis about the Ecliptic Pole. A precession is when a spinning body's axis of rotation itself executes the motion of sweeping out a CONE. Precession is what a toy top does.

Precession of a toy top.

We will not detail the physics of precession here. We just note that a spinning body has a resistance to having its axis of spin changed. This is why GRYOSCOPES (which are just spinning masses) are used to stabilize orientations of spacecraft and other things. A more more common example is a BICYCLE. Everyone knows that a stationary upright bicycle is unstable. But if the wheels are turning, it is stablized.

Alien stablized on a bicycle.

A NON-SPINNING TOP set on its tip is in unstable equilibrium and any perturbation causes gravity to topple it. But if it is spinning, then the spin stablizes top to a degree. In way complicated to describe, but easy to observe, gravity instead of toppling the top just causes it to precess. Ideally gravity cannot change the amount of spin (angular momentum magnitude to be technical), but it will continually change its orientation in space. Now a toy top will also have friction between tip and ground and this will reduce the kinetic energy of the coin and thus the stabilization and it will fall over.

A very common example of the precession effect is a RINGING COIN. Set a coin on edge and let it just fall over: the fall is relatively quick. But set the coin spinning and the time of fall is much reduced as the coin rings. A ringing coin motion is actually very complex, but at least part of it the precession effect.

As a foresaid, we will not go further into the physics. But it's sufficiently tricky that it's not taught in 1st year physics and many physicists (like moi) who don't deal with rotational motions much know only the simplest analyses.

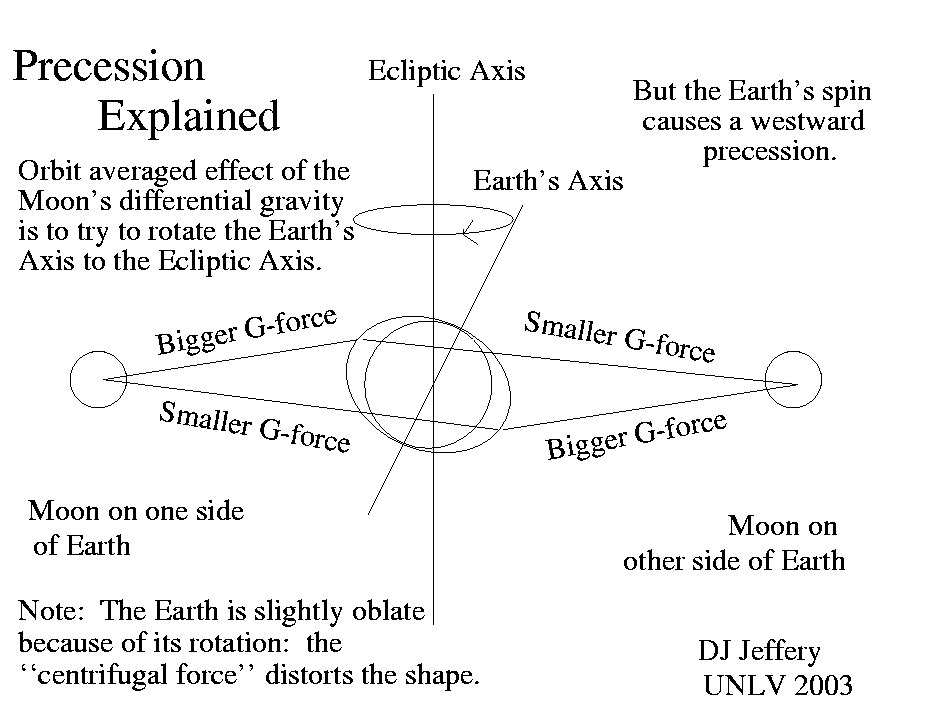
But why does the Earth precess? Because of the Earth's rotation, it is not perfectly spherical. It's shape is slightly oblate: it's polar radius is about 1/300 smaller than it's equatorial radius. This causes the gravitational forces of the Moon, to a lesser degree of the Sun, and to a much lesser degree of the planets to try to rotate the Earth's axis toward the Ecliptic Axis.



The orbit-averaged effect of the Moon, for example, is to pull gravitationally in a differential manner of the Earth's lobes. Gravity falls off with distance. So as the diagram illustrates the Moon tries to pull the Earth's axis to the Ecliptic axis. (Here we assume for simplicity that the Moon's orbit is in the Ecliptic Plane exactly. Actually it is tilted slightly by 5 degrees, 9' [Se-33].) The Sun has a similar but smaller effect; the planets a much smaller effect. But the Earth's axis doesn't get pulled to the Ecliptic Axis. Because of the Earth's spin a westward precession of the Earth's axis is set up. Westward on this diagram means the north end of the Earth's axis is coming up from the screen.

The precession effect is actually very small. The current rate of precession would lead to a complete cycle with a PERIOD OF 25,770 YEARS. But in fact the precession rate is increasing slightly.

Now why if the Earth's AXIS is precessing is the effect called the precession of the EQUINOXES.



Well if your coordinates (including the NCP, SCP, and Celestial Equator) are fixed with the Earth's axis, then the precess with the Earth. If you take an outside view with the Ecliptic Axis vertical and the Ecliptic horizontal, then the whole Earth-based coordinate system precesses westward relative to the fixed stars as the diagram to the right illustrates. This means that the points where the equinoxes cross Ecliptic move westward along the Ecliptic.



The zodiac constellation in which the Vernal Equinox happens to be located in the mythology according to the musical Hair defines the astrological age. In 2500 BC, the Vernal Equinox was in Taurus; in 500 BC (when horoscopic astrology was being set up [No-39,41]), it was in Aries; nowadays, its at the western end of Pisces; in about 2500, it may be Aquarius depending on how you make the call: see the sky chart Donald V. Etz. for the progression of the Vernal equinox. Anyway the dawning of the Age of Aquarius (when ``love will steer the stars'') still seems some way off.

ANCIENT ASTRONOMERS who kept centuries of records in some form probably appreciated to some degree that equinoxes were shifting. This is true even of prehistoric, preliterate people if they kept records effectively in stone monuments like Stonehenge (No-5). However, the historical astronomer definitely recognize the precession and quantify it was HIPPARCHOS (2nd century BC) (No-99). The physical explanation of the precession was first given NEWTON (1643--1727) in his Principia in which he detailed his 3 laws of motions and his law of gravity (No-370).

The Earth actually exhibits a NUMBER OF MOTIONS: daily spin, yearly revolution, precession of the axis, variation in orbital eccentricity, revolution of the perihelion-aphelion line, and other smaller motions. The major motions at least are periodic---but only to a degree. Every motion is actually evolving at least slowly because of complex gravitational perturbations along with geological and subtler effects. The paper by Donald V. Etz for the Astronomical Society of the Pacific (ASP) gives a nice review of these motions without going into physics detail.