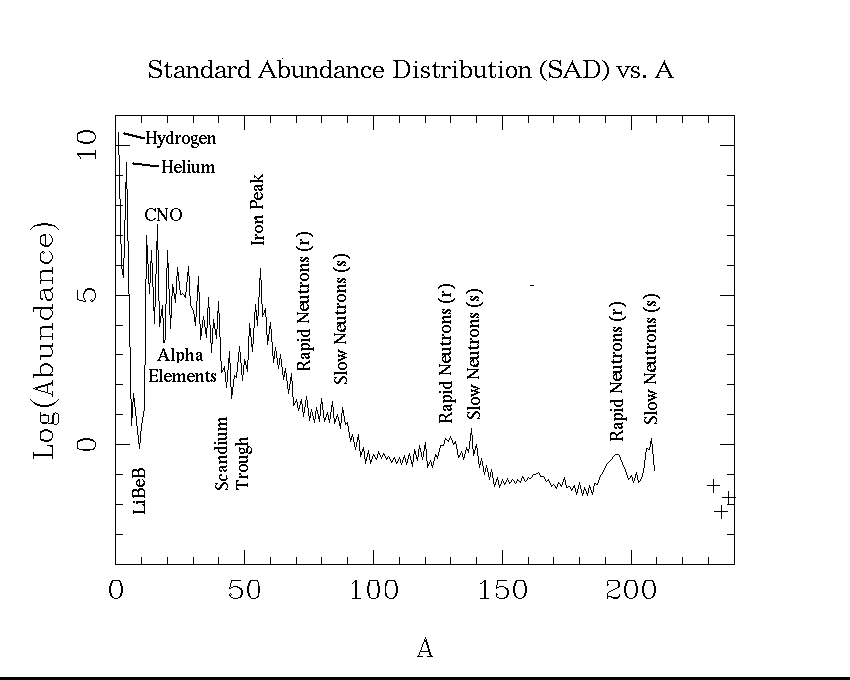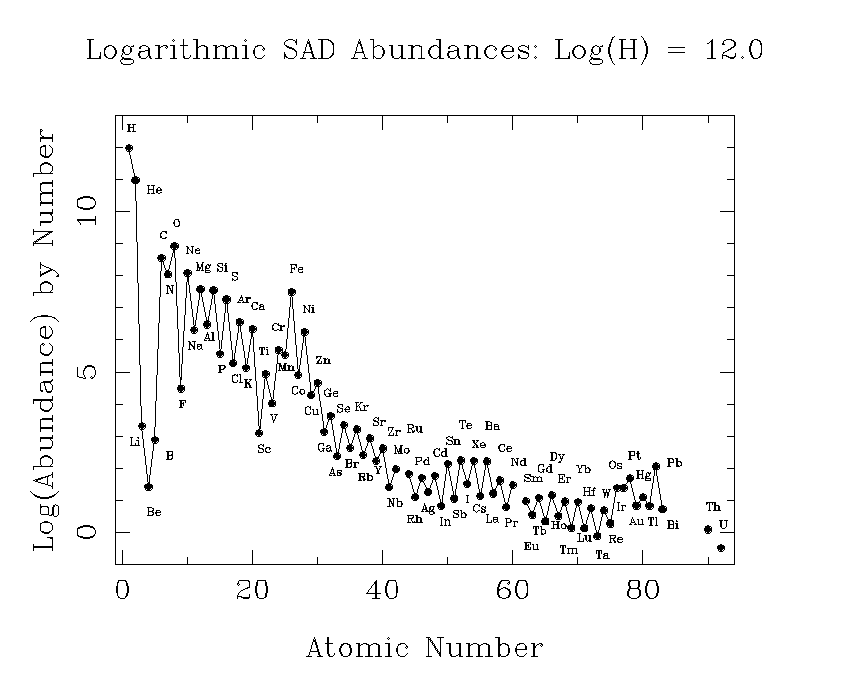

This plot shows our best estimates of the abundances of the elements as they now exist in the sun. This is also what we think the relative abundances were in the primordial solar nebula. It is customary to choose one element as a standard, and give the abundances of other elements relative to it. In astronomy, hydrogen is the standard element, and its abundance is arbitrarly set to 1012.
A tabular version of the SAD is also useful.
Possibly the most noticable feature of this plot is the sawtoothed pattern. Elements with an even number of protons (Z) are typically more abundant than those with and odd number. The only exceptions are hydrogen (Z = 1), which was made in the big bang and is the most abundant element in stars, and Be (Z = 4), which is less abundant than either of its odd-Z neighbors, Li (Z = 3) or B (Z = 5).
There are two basic reasons why most elements with even Z are more abundant. First, elements with even Z have more isotopes. This can be seen from the nuclide chart. Another reason is that nuclei are especially stable if nucleons can "pair up" with their spins in opposite directions. This works for neutrons as well as for protons, but if Z is even, the protons can pair up, while if Z is odd, there must always be an unpaired proton. This abundance alternation is often called the odd-even effect.
The overall pattern is one of decline, with some valleys and peaks. This is because the two most abundant elements, hydrogen and helium, were made at the birth of the universe. Heavier elements were mostly made in stars.
The trough at Li, Be, and B, occurs because these elements are destroyed in stars. We actually think they were mostly made in cosmic ray interactions in the interstellar medium, rather than in stars. The peak at iron comes because of the special stability of this element. Nuclei are held together by the strong nuclear force, which is most effective at short distances. The electrostatic repulsion of the nuclear protons opposes this, and tries to disrupt the nuclei so to speak. If nuclei get too heavy, the electrostatic force wins. This is why there are no stable elements beyond bismuth (Z = 81). It turns out that the optimum of the nuclear force occurs for Z = 26, iron, and this stability is reflected in what abundance workers call the iron peak.
Apart from the special effects due to nuclear properties, the abundance of one element is closely related to the abundance of its neighbors. This is because in the synthesis of the elements, heavier ones are made from lighter ones. There is a slow build up. You need to contrast this with the situation in the earth's crust, where chemical properties play a large role in the abundances.
Elements beyond the iron peak cannot be made by processes that can act as a source of stellar energy. Elements lighter than iron, can fused to form heavier elements and at the same time furnish energy. This is the principle of the hydrogen bomb, and the energy currently supplied by the sun. Heavier elements can only supply energy by fission. This is the principle of the original uranium bomb.
How then are the heavier elements made? The answer is that they are made by neutron addition processes. The sites of these processes are surely stellar interiors. The signature of these neutron addition processes are best viewed on a plot of cosmical abundance as a function of the mass number A = Z + N. Here is such a plot. Notice the bumps and spikes beyond the iron peak at A = 56. Just how these peakes come to be at these particular places will be discussed in a course offered in the winter term on the history of the chemical elements.