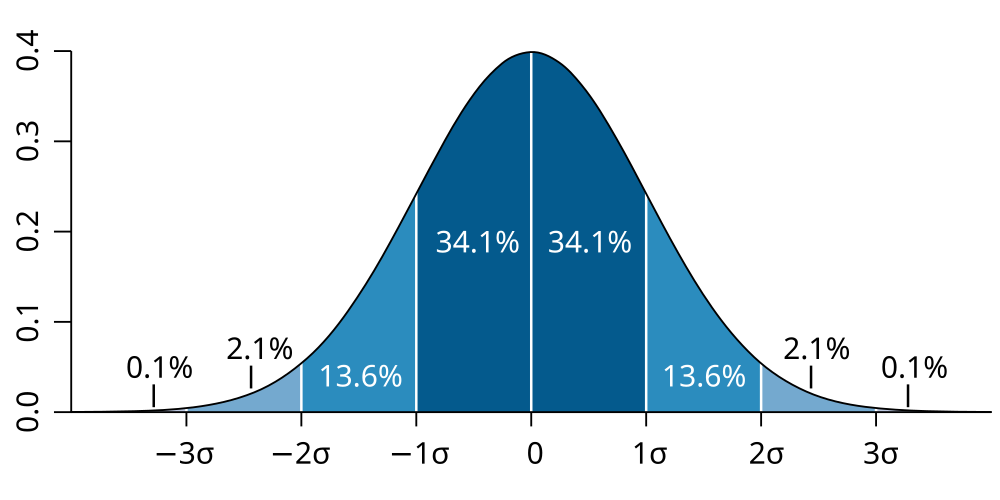
Caption: The Gaussian distribution (AKA the normal distribution, AKA the bell curve).

Features:

1. A probability distribution describes the statistical frequency of some variable that forms a statistical population

2. The Gaussian distribution is a particular probability distribution that applies approximately to many physical systems and other kinds of system, and exactly to a few.

   There are good reasons why it has wide application---but we won't go into that here.

3. The Gaussian distribution is characterized by two parameters: the mean (often given the symbol Greek lower-case letter μ (pronounced mu) and the standard devation.

4. A standard devation (given the symbol Greek lower-case letter σ (pronounced sigma and often just called sigma) of probability distribution is a standard measure of the width of the probability distribution.

   For the Gaussian distribution, ∼ 68 % of the population is within one σ of the mean, ∼ 95 % of the population is within 2σ of the mean, and ∼ 99.7 % of the population is within 3σ of the mean.

5. The grades of a class of Gaussian distribution. Thus, the fitted Gaussian distribution can be used to assign letter grades automatically.

   How is this done?

   The instructor calculates the μ and σ for the actual class. Then for example, the instructor decides that he/she wants about 16 % of the class to have A's. From the curve in the diagram, the instructor knows that about 16 % of the Gaussian distribution, there won't be exactly 16 % A's assigned, but usually the number will be close to 16 %.