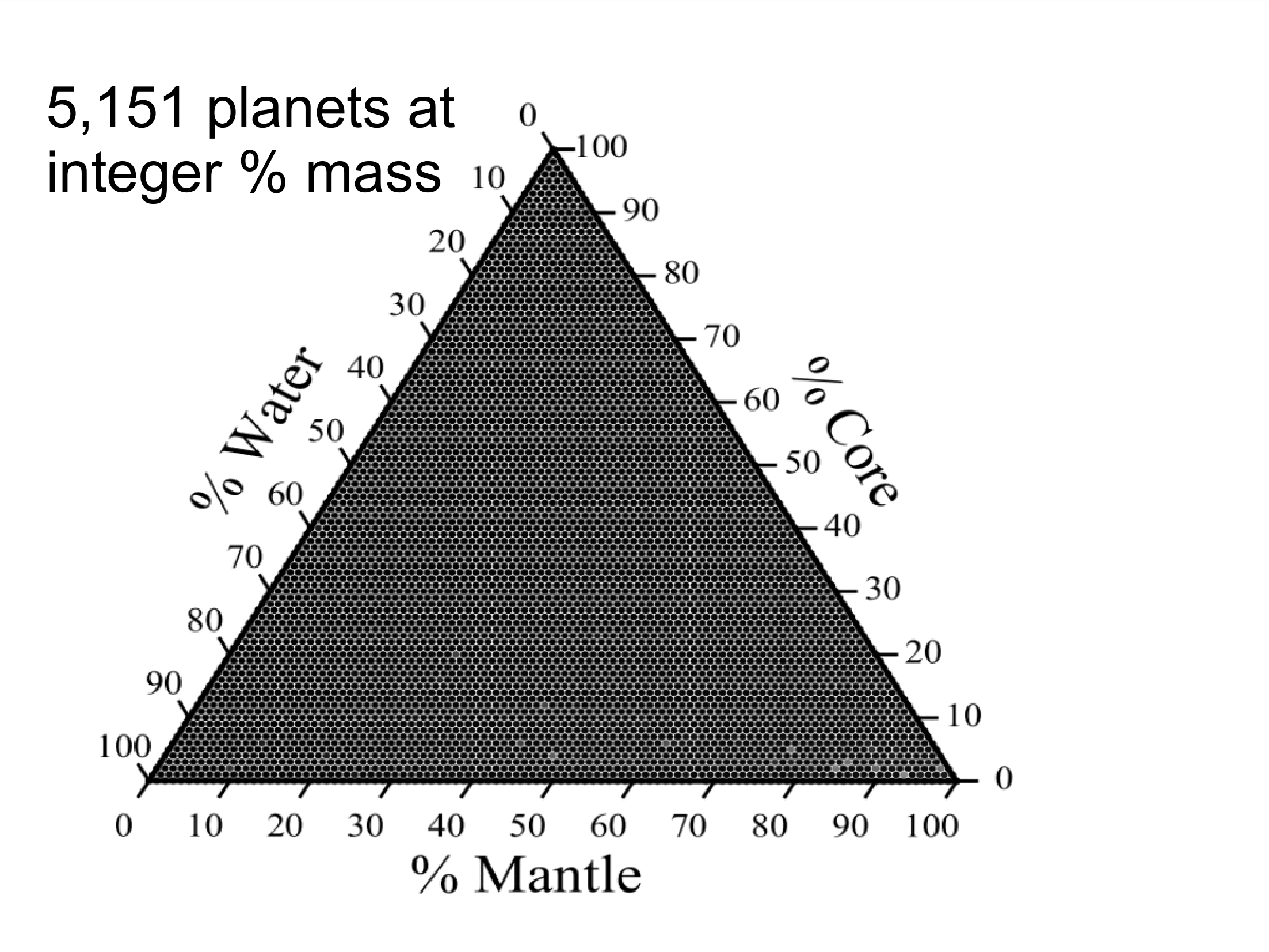
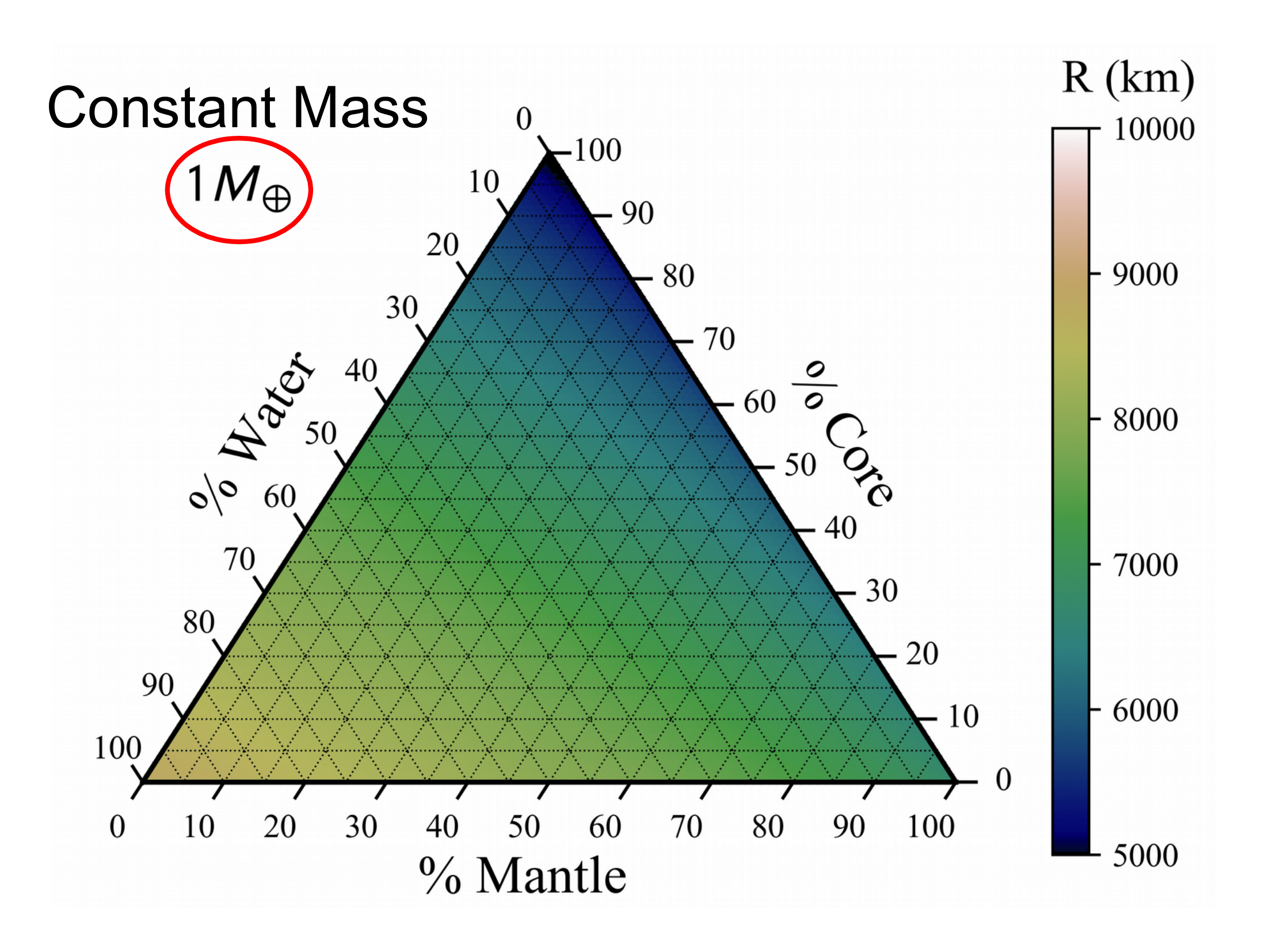
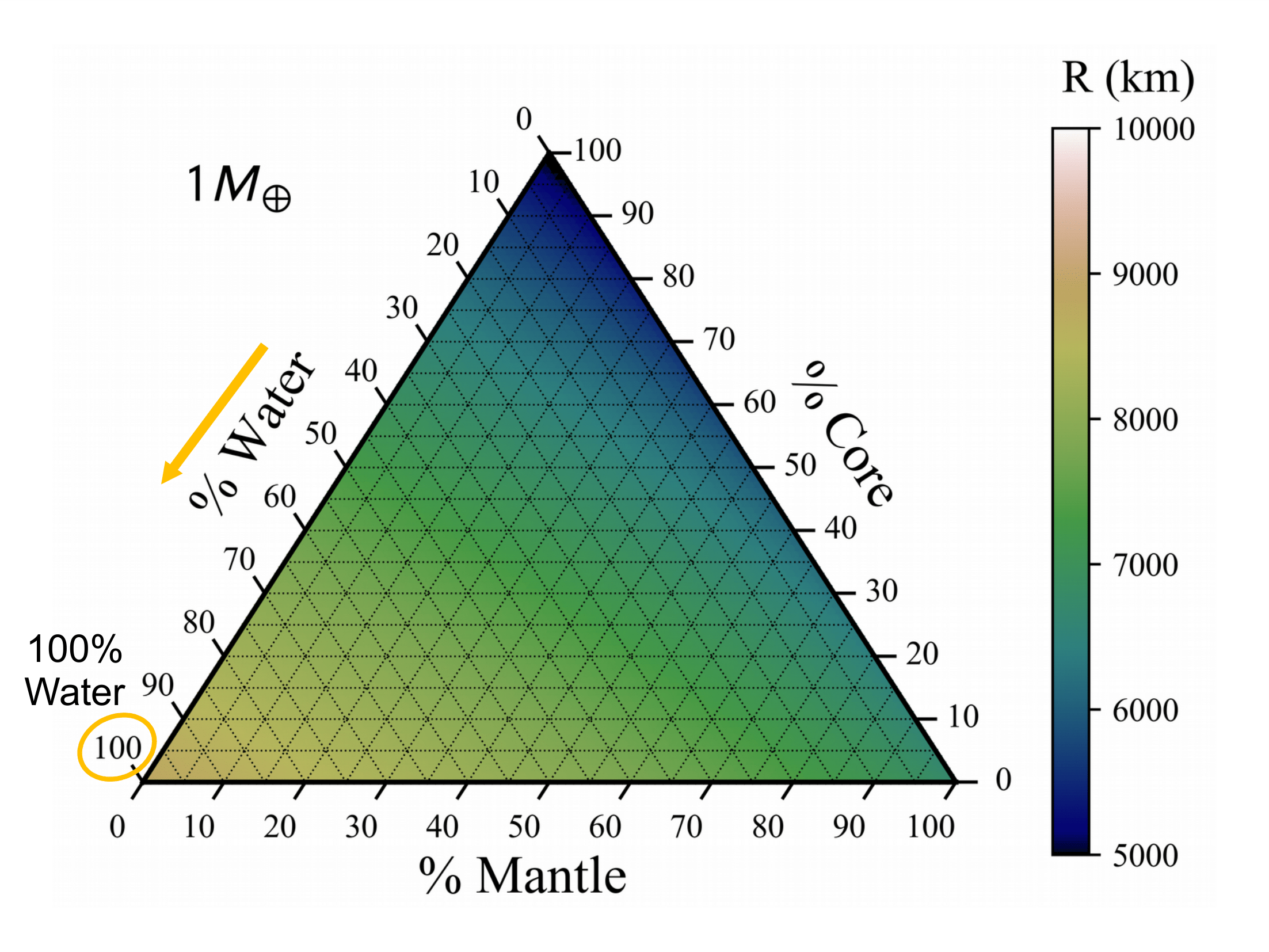
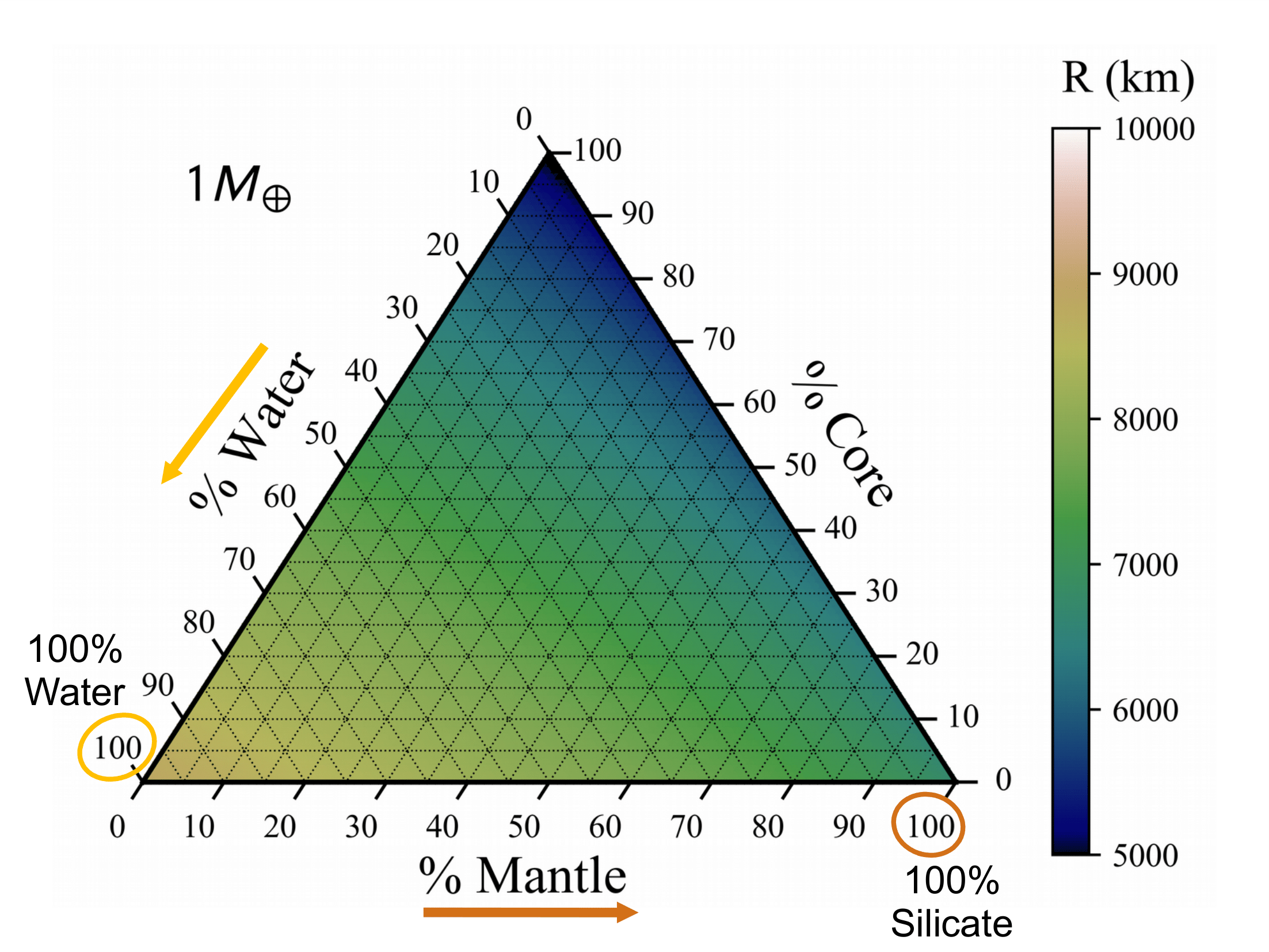
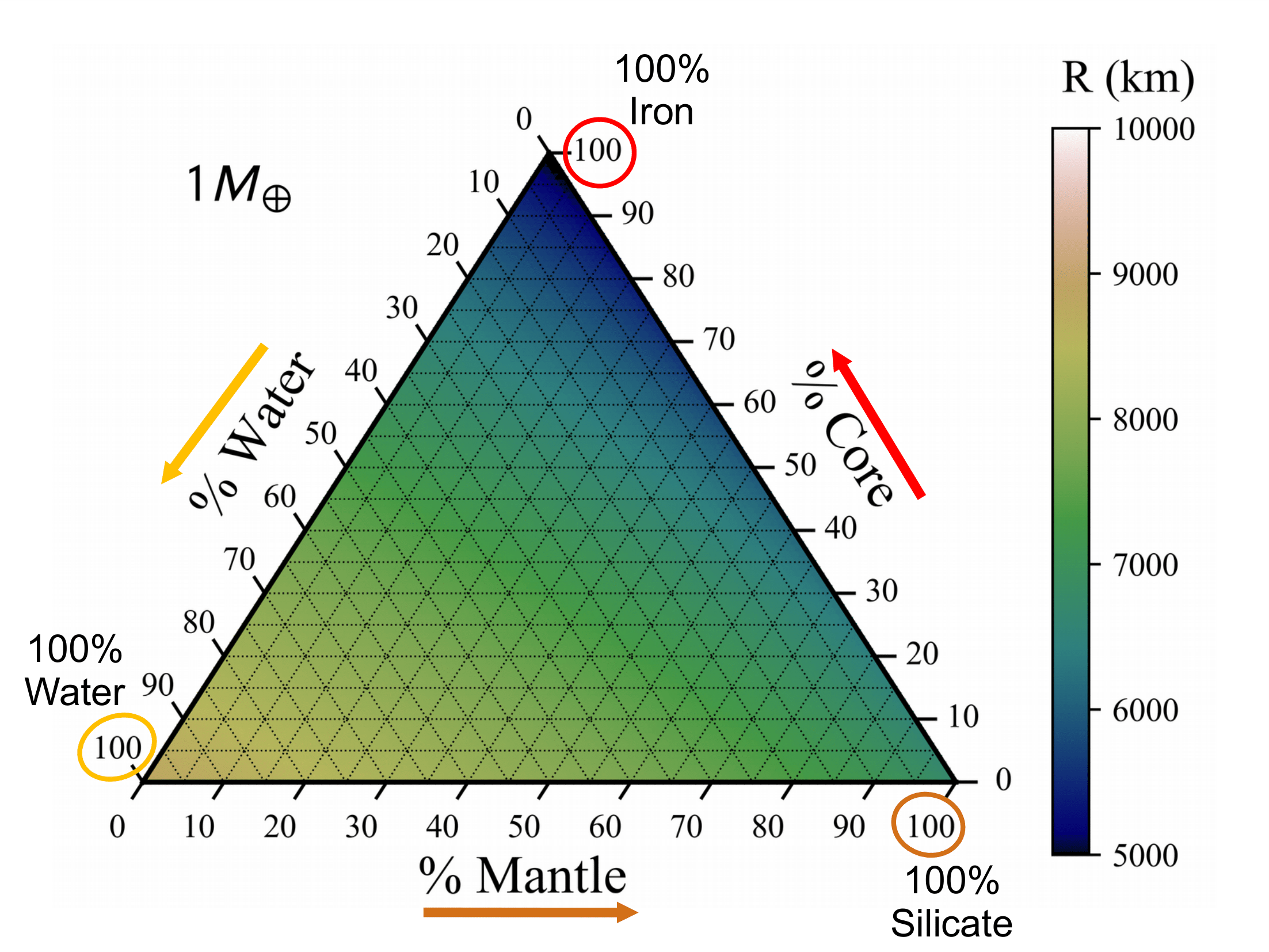
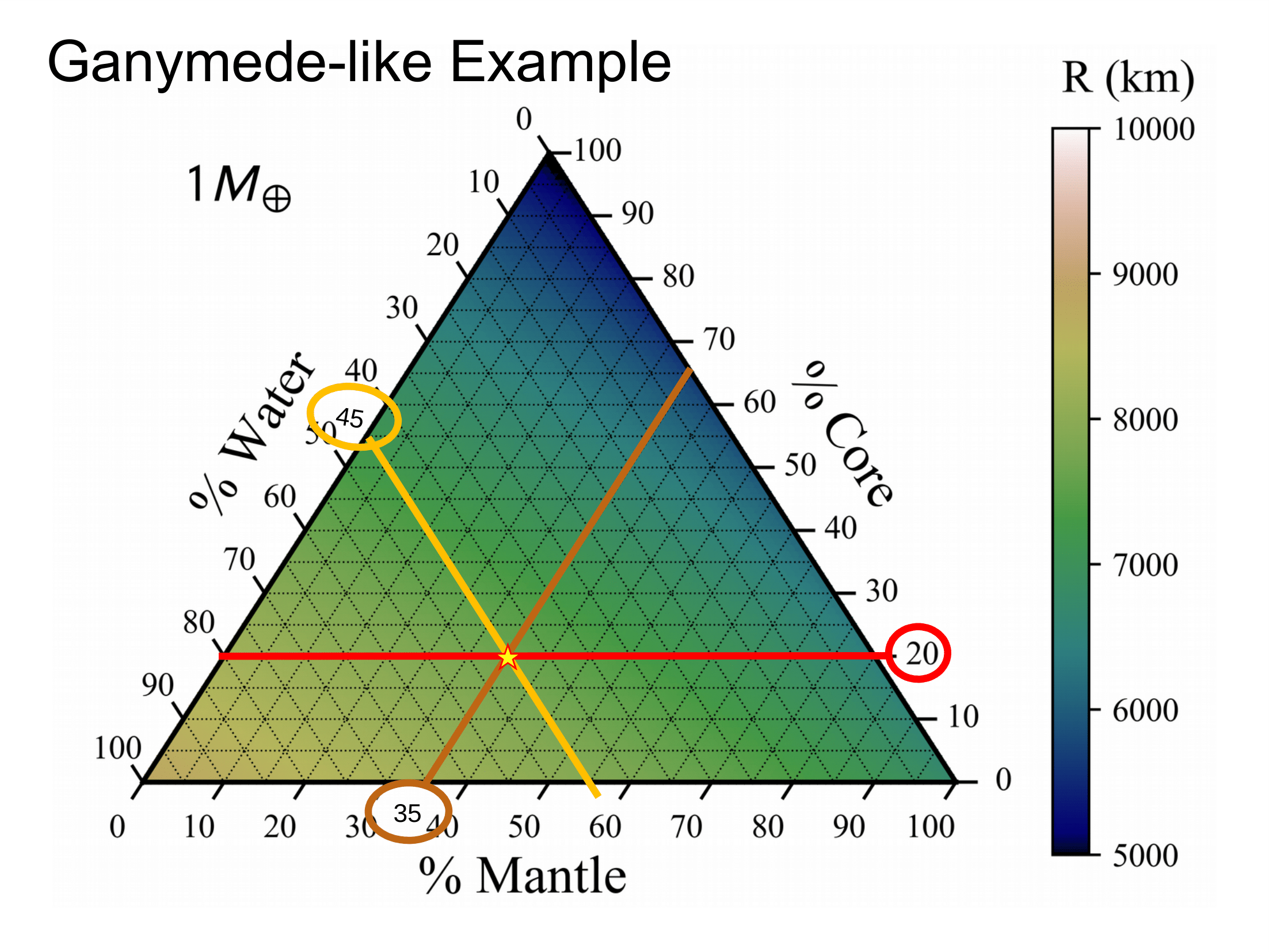
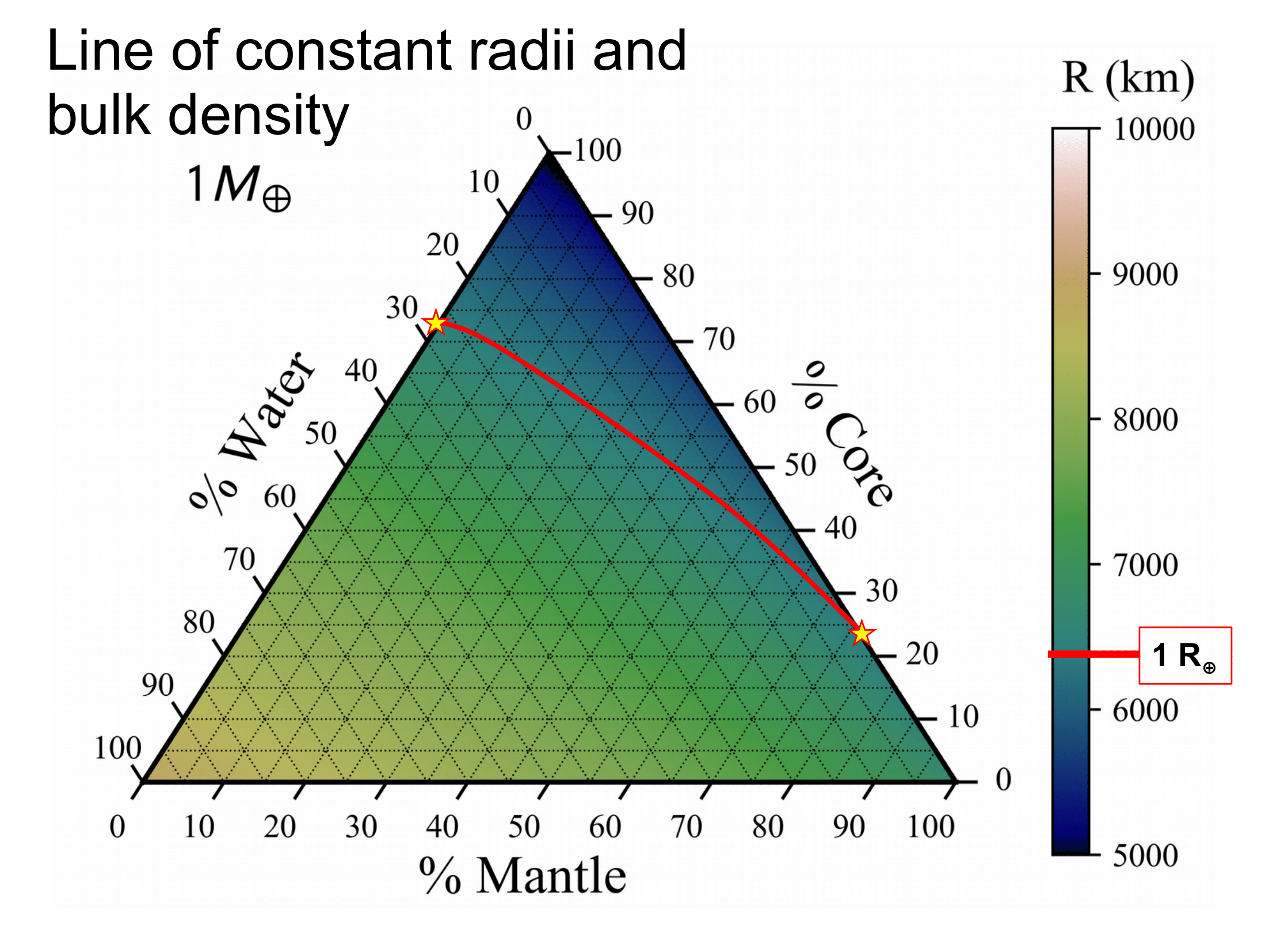
Ternary diagrams are a great way to plot 3 variables that add to a constant on an equilateral triangle.
Our diagrams show the entire range of compositions for a 3-layer differentiated planet.
The axes show the % of mass in the corresponding layer.
Scroll through this to get an idea of how our ternaries work:
MAGRATHEA: Terrestrial Planet Interior Solver
and the Degeneracy of Interiors
David R. Rice1, Chenliang Huang (黄辰亮)2, and Jason H. Steffen1
1University of Nevada, Las Vegas, 2The University of Arizona

Abstract
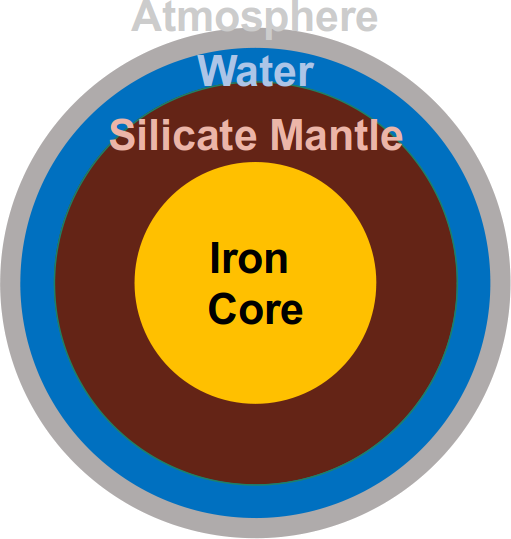
MAGRATHEA is a newly-developed planet structure code for differentiated terrestrial planets. Our open source code supports spherically symmetric layers of iron, rock, ice/water, and ideal gas (with more options planned in future versions). MAGRATHEA integrates the hydrostatic equation to find the planet radius and pressure, density, temperature, and phase as a function of radius for a planet with the designated mass in each differentiated layer. Our code features enhanced flexibility to change the equations of state in each layer allowing for collaboration with high pressure physicists. The inferred densities of observed exoplanets allow for diverse compositions. Mass-radius relationships fail to capture the range of possible interiors and compositions a given planet may have. With MAGRATHEA, we explore planetary radii across a large parameter space of planet interiors.
Model
We consider planets which are spherically symmetric and fully-differentiated. Given the mass of each layer the code returns the pressure, density, and temperature at enclosed mass, m, by solving:
1. Mass Continuity
\(\frac{dr(m)}{dm} = \frac{1}{4 \pi r^2 \rho(m)}\)
2. Hydrostatic Equilibrium
\(\frac{dP(m)}{dm} = -\frac{G m}{4 \pi r^4}\)
3. Isothermal or Isentropic temperature profile. For isentropic:
\(S(\rho,T) = S(\rho_0,T_0) \equiv S_0\)
where \(S_0\) is the entropy at a reference point.
4. Equation of state (EoS)
\(P(m) = P(\rho(m),T(m))\)
which describes the pressure for a layer as a function of the density, temperature, and composition.
The boundary conditions of the model are \(r=0\) at \(m=0\) and \(P = 1~bar\) at \(m=M_p\). The temperature at the surface is user-defined. Jumps in temperature may also be defined at the boundaries between layers.
MAGRATHEA
The code is written in C++ and designed to enhance the ease-of-use, speed, and customization of interior solvers. We solve the two-point boundary value problem by the shooting method to a fitting point using RKF-45. There are several input modes including the regular solver, a quick temperature-free solver, a bulk input mode, and an MCMC method for testing EoS errors.
Equation of State Customization
MAGRATHEA's key feature is our transparent structure for EoSs. Users can easily change and add additional equations for their planets. This empowers our collaboration with high-pressure physicists to include the most up-to-date experimental results.
Many types of EoS are accepted including tabulated (as in Seager et al. 2007), Birch-Murnagham, Vinet, Holzapfel, and Keane.
Figure 1: To demonstrate different EoS choices, we plot the density as a function of radius inside a one Earth-mass planet with 33% of the mass in the core. Blue, Magrathea's Default planet with hcp-Fe core (Smith et al. 2018) and P-Pv mantle (Oganov & Ono 2004; Sakai et al. 2016) at 300K. Green, planet with Fe-Si alloy core (Wicks et al. 2018) and PREM mantle (Zeng et al. 2016). The radius of the earth-like planet differs by 1.3%. Legend also lists the time for one run averaged over 100 runs. The non-default planet runs faster because these EoS choices have no thermodynamic information. These times may improve in the final version.
We have over 30 EoSs implemented in the code. Future additions will include liquid silicates and more complex atmospheres.
Degeneracy of Interiors
"All you really need to know for the moment is that [planets are] a lot more complicated than you might think, even if you start from a position of thinking it’s pretty damn complicated in the first place." ~Douglas Adams-ish
Mass-radius relationships have been used extensively in describing planet composition. However, these relationships are not unique when considering a planet with three or more layers. For a three-layer planet, ternary diagrams provide a way to visualize the interior structure parameter space for a planet with a certain mass. The axes of the ternary depict the percentages of mass in the three layers—core, mantle, and water. Ternary diagrams have been used for exoplanet interiors in several works including Rogers & Seager 2010.
Use these drop-downs to show a corresponding ternary created with MAGRATHEA:
Mass
\(M_\oplus\)
Surface Temp. K
Atm. Mass %
Figure 2: The ternary shows the possible radii in Earth-radii of the user-selected planet across the entire range of composition. Marked and labeled is an Earth-like interior with 30% core and 70% mantle by mass. The atmosphere mass drop down adds a H/He ideal gas atmosphere with the corresponding mass percentage taken evenly from the three layers. Each ternary is made up of 5,151 planets simulated with MAGRATHEA at integer mass percentages. Some extreme cases may still cause errors and show up as white. Plotting package is included in our code and makes use of python-ternary by Harper et al. 2015.
TRAPPIST-1f 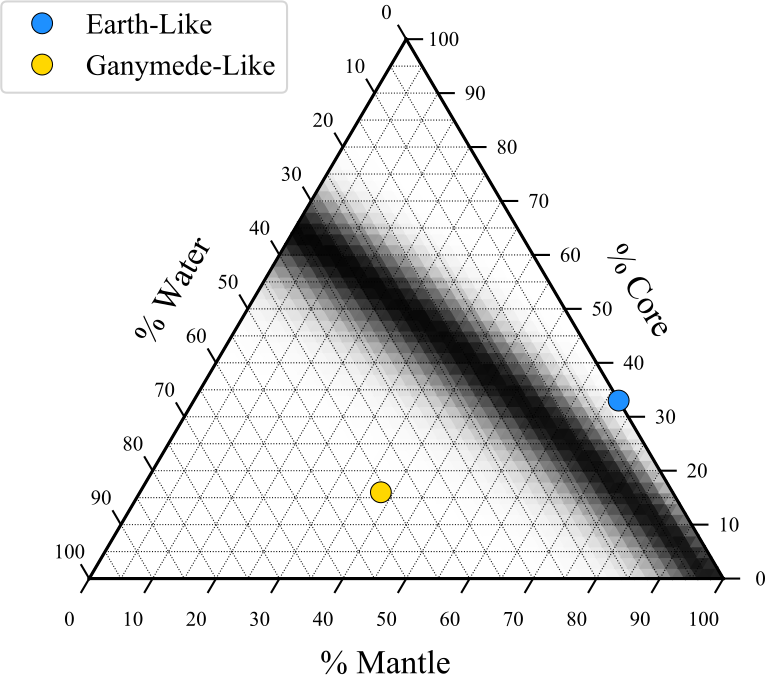
Using MAGRATHEA, we combine the observational errors in mass and radius from Grimm et al. 2018 to find the most likely interior for Trappist-1f. On the figure, right, we plot the posterior of interior structure where black is higher probability.
Because of Trappist-1f's low bulk density, we see that the planet most likely has a significant water/ice layer. How much water is needed is dependent on the core/mantle size. Alternatively, you could achieve this bulk density with an atmosphere.
Become a Magrathean (Coming Soon):
https://github.com/Huang-CL/Magrathea
References
Grimm, S. et al., 2018, A&A, 613, A68
Harper, M. et al., 2015 Zenodo 10.5281/zenodo.594435
Oganov, A. & Ono, S., 2004, Nature, 430, 445
Rogers, L.A. & Seager, S., 2010, ApJ, 712, 974
Sakai, T. et al., 2016 Sci. Rep., 6, 22652
Seager, S. et al., 2007, ApJ, 669, 1279
Smith, R.F. et al., 2018, Nature Ast., 2, 297
Wicks, J.K. et al., 2018, Sci. Adv., 4, eaao5864
Zeng, L. et al., 2016, ApJ, 819, 127