Chapter 9
Basic Properties of Stars
Measure of brightness (Hipparchus)
By agreement, absolute magnitude is apparent magnitude at a standard distance - 10 parsecs
Parsec = 3.26 light years
Absolute mag. of sun = +4.8
Range in absolute magnitude for stars
~ -10 to +17 mag.
Distances
Basic, difficult problem.
Geometric methods basic and most reliable - for nearby stars only.
Used to calibrate secondary methods.
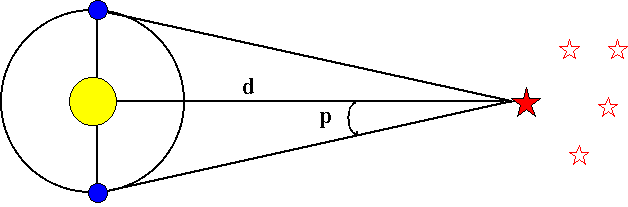
Trigonometric parallaxes

Parsec: distance at which star has a parallax of 1 arcsec.
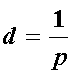
d (distance) in parsecs.
ex.: p = 0.10 second of arc (arcsec):
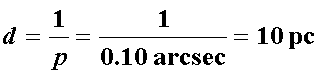
From earth, measure only parallax greater than 0.01 arcsec (distance less than 100 pc).
Hipparcos - parallax ~ 0.001 arcsec (distance to 1000 pc)
Spectroscopic parallax - derive absolute magnitude from spectrum, measure apparent magnitude
Magnitude - distance relation:
mv - Mv = -5 + 5(log10d)
Luminosity: Amount of energy emitted in one second at all wavelengths.
Use Mv, correct for non-visible wavelengths.
Absolute bolometric magnitude:
Mbol: Absolute magnitude including all wavelengths.
Compare Mbol star to Mbol sun (star = observed star) to get stellar luminosity.
ex.: Luminosity of sun, Lsun = 4x1026joules/sec
Color and Temperature
Color and temperature of stars related
Black body: absorbs and re-emits all radiation that falls on it. Spectrum depends only on temperature. Idealized, does not really exist.
Stars can be represented as black bodies.
Hot stars bluer than cool stars.
λ in micrometers (microns, Ám) = 10-6 meter
T temperature in Kelvin
Estimate star's temperature by measuring color:
Luminosity, Size, Temperature
Luminosity of a star depends on temperature and size (surface area)
Amount radiated from every square meter equals σ x T4
{Stefan-Boltzmann Law}
The hotter the star, the more energy radiated per square meter
Total amount radiated (luminosity)
L = 4πR2σT4
R is star's radius, T is temperature
If measure L, T can estimate R
Spectral Classification
Strength of lines determined by temperature, as well as chemical abundance
Group spectra according to strength of various lines
Line strengths define temperature sequence:
Stars of the same spectral type may be at different stages of evolution, vary greatly in brightness, density of atmosphere.
Hertzsprung-Russell Diagram
Plot temperature against luminosity (or equivalent parameters)
Stars found in certain parts of H-R diagram
Main sequence - class V stars - converting H -> He in their centers
Red giants - class III, cool and big, evolved stars
Supergiants - evolved, class I, very bright
White dwarfs - small, hot stars. End of stellar evolution for most stars.
Mass range in stars: 0.08 - 100 M (solar masses)
Stellar Motions
Space velocity - motion relative to the sun ~ tens of km/sec
Radial velocity, transverse velocity
Proper motion - angular shift in star's position on sky due to transverse velocity.
Binary and Multiple Stars
Binary star - 2 stars bound by mutual gravitational attraction. More than half of stars are in binary or multiple systems
Binaries only way to directly measure masses of stars
Visual binary - can resolve both stars in binary
Observe period, average distance between stars, distance of each star from center of mass
Calculate masses using Kepler's Third Law
Unresolved Binaries
Astrometric binaries - identify by 'wobble' in proper motion
Spectroscopic binaries - identify by combined spectrum. Two sets of absorption lines - shift due to orbital motion. (Single-line binaries.)
Eclipsing binaries - orbit nearly edge-on, stars pass in front of each other. Periodic changes in brightness of the system.
Eclipses can be used to estimate stellar radii
Roche lobes - define volume controlled by individual stars in binaries
If star overflows Roche lobe, matter can be transferred to other star
Contact binary - both stars fill Roche lobes, surfaces in contact
Variable stars
Change in brightness
Pulsating variables - expand and contract regularly.
Cepheid variables : 1 - 80 day periods.
Brighter Cepheids have longer periods.
Used to get distances to nearby galaxies
Cataclysmic Variables - sudden increases in brightness - flare stars, novae, supernovae
Prof. Donna Weistrop
University of Nevada, Las Vegas