Crystal Structure Prediction and its Application in Earth and Materials Sciences: Theory of the quasi-harmonic approximation

3.3 Theory of the quasi-harmonic approximation

If we treat the atom in a harmonic potential, the model would fail in explaining thermal expansion, as the equilibrium distance between atoms would be invariant with temperature. The quasi harmonic approximation(QHA) is a phonon-based model used to treat frequencies as volume dependent so as to account for thermal effects.

For a lattice, the Helmholtz free energy 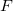$F$ in the QHA is,

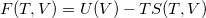$\begin{equation} \label{qha} F(T,V) = U(V)-TS(T,V) \end{equation}$

(62)

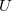where $U$ is the internal lattice energy, 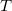$T$ is the absolute temperature, 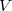$V$ is the volume and 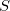$S$ is the entropy due to the vibrational degrees of freedom.

This entropy term is from lattice vibration.

$\begin{equation} \label{qha2} S(V) = -N\sum _{k,i}k_ B\text {ln}[1-\text {exp}(-\frac{h\upsilon _{k,i}(V)}{k_ BT})] + N\sum _{k,i}\frac{1}{T}\frac{h\upsilon _{k,i}(V)}{\text {exp}(-\frac{h\upsilon _{k,i}(V)}{k_ BT})-1} \end{equation}$

(63)

The Gibbs free energy of the system is a function of temperature and pressure.

$\begin{equation} \label{qha3} G(T,P) = \text {min}[U(V)-TS(T,V)+PV] \end{equation}$

(64)

Since volume dependencies of energies in electronic and phonon structures are different, volume giving the minimum value of the energy function in the square brackets shifts from the value calculated only from electronic structure at 0 K. The increase in temperature can changes the volume dependence of phonon free energy, and then the equilibrium volume. This is considered as thermal expansion under QHA.

From the dynamical study of the atoms one can get more insight into many important physical properties such as phase transitions, thermal expansion, and thermal conductivity and other transportation properties. The excited lattice vibrations can often be described as harmonic, below the Debye temperature. These vibrations can be described as linear combinations of vibrational eigenfunctions with discrete energies also known as phonon. The phonons are described by three parameters, wave vector, polarization vector, and energy. The information about the vibration of atoms along all the three directions is given by the polarization vector. The dispersion relation of the phonon spectrum, is an important quantity in the study of the physical properties of a solid system. Above the Debye temperature, the higher order terms in the expression have to be taken into account, and the lattice vibrations are no longer harmonic and interaction of phonons can occur. If there is a small anharmonicity, this can be solved using perturbation theory. But if the anharmonicity is large, molecular dynamics simulation is a good option. With this technique, one can study thermodynamic properties and phase transitions.