Research Interests of Professor Tao Pang

Professor Tao Pang and his group are developing and applying theoretical and computational methods to study novel materials and structures, including cold atoms and molecules, supersolids, and highly correlated systems. The main techniques used in his group include path-integral and diffusion quantum Monte Carlo methods and other first-principles approaches. The following are highlights of a couple of systems under study.

The clusters of atoms and molecules at extremely low temperature are fascinating systems created recently with laser cooling and trapping. They are ideal systems to study quantum many-body effects in a controlled manner because the interaction between two particles can be tuned experimentally.

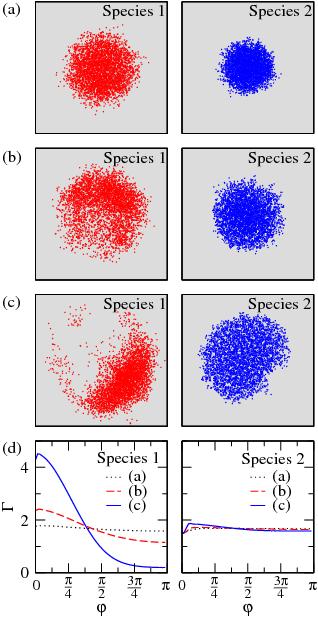
We have studied the trapped cold atoms with the path-integral quantum Monte Carlo method and evaluated the transition temperature of the Bose–Einstein condensation, condensation fraction, and specific heat of the systems under various conditions. Here we show some snapshots of multi-exposures of the particles viewed along the z direction for each species in a double-condensate mixture, confined in a trap with m₂/m₁=4, N₁=N₂=100, a₁₁=0.2, and a₂₂=0.4, for different aspect ratio lambda=omega_z/omega_perp (on the left) with (a) lambda=1; (b) lambda=4; and (c) lambda=16, and for different ratio eta=a₁₁/a₂₂ (on the right) with (a) eta=1/3; (b) eta =1/2; and (c) eta=1. The corresponding in-plane angular pair-correlation functions Gamma_i(phi) are shown in (d). The planar symmetry in each of the two condensates is broken if lambda is not equal to 1; the asymmetry becomes more severe when lambda is further away from 1, especially for the lighter species.

If you wish to know more about our work on cold atoms, please see the following articles.

References:

1. S. Pearson, T. Pang, and C. Chen, "Bose–Einstein Condensation in One-Dimensional Power-Law Traps: A Path-Integral Monte Carlo Simulation," Physical Review A 58, 1485–1489 (1998).
2. S. Pearson, T. Pang, and C. Chen, "Bose–Einstein Condensation in Two-Dimensions: A quantum Monte Carlo Study," Physical Review A 58, 4811–4815 (1998).
3. S. Pearson, T. Pang, and C. Chen, "Critical Temperature of Trapped Hard-Sphere Bose Gases," Physical Review A 58, 4796–4800 (1998).
4. H. Ma and T. Pang, "Condensate-Profile Asymmetry of a Boson Mixture in a Disk-Shaped Harmonic Trap," Physical Review A 70, 063606 (2004).
5. H. Ma and T. Pang, "Path-Integral Quantum Monte Carlo Study of a Mixture of Bose-Einstein Condensates," Physics Letters A 351, 92–96 (2006).

The breakthrough in the torsional oscillator experiment by Kim and Chan in 2004 on solid ⁴He has the entire physics community excited about the potential of their observation being the first detection of the nonclassical rotational inertia (NCRI) and thus supersolidity in a quantum solid. Theorists have been trying to come up with a decent explanation while experimentalists have first confirmed their discovery and then continued to discover some other peculiar properties of the system. So far a coherent picture of what is going on in solid ⁴He is still missing. The main objective of our work is to seek a thorough understanding of the properties of quantum solids through quantum Monte Carlo simulations.

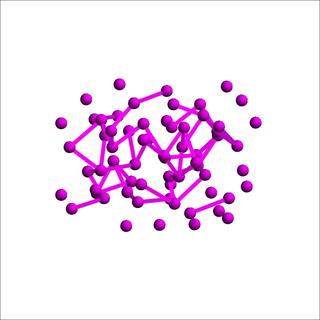
We have obtained preliminary results with diffusion quantum Monte Carlo method. The hcp lattice with 64 sites in the simulation box and the final configuration of one of the simulation runs with the site-based guide wavefunction are shown below. The final configurations in the runs with the particle-based guide wavefunction have similar characteristics. After we carry out a detailed analysis of the particle distributions over the entire course of simulation, we will know more about the structures of the many-boson system. A preliminary analysis of the data shows that the quantum fluctuation is extremely strong in the system and the particles are away from lattice sites quite often.

If you wish to know more about supersolidity, please see the following references.

References:

1. E. Kim and M.H. Chan, "Probable Observation of a Supersolid Helium Phase," Nature 427, 225–227 (2004).
2. N. Prokof'ev, "What Makes a Crystal Supersolid?," Advances in Physics 56, 381–402 (2007).
3. D.E. Galli and L. Reatto, "Solid ⁴He and the Supersolid Phase: From Theoretical Speculation to the Discovery of a New State of Matter? —A Review of the Past and Present Status of Research—," Journal of the Physical Society of Japan 77, 111010 (2008).
4. B. Hunt, E. Pratt, V. Gadagkar, M. Yamashita, A.V. Balsky, and J.C. Davis, "Evidence for a Superglass State in Solid ⁴He," Nature 324, 632–636 (2009).
5. P.W. Anderson, "A Gross–Pitaevskii Treatment for Supersolid Helium," Science 324, 631–632 (2009).